Finitely presented groups are defined by a finite set of generators and a finite set of relations among those generators, making their structure easier to analyze compared to infinitely presented groups. These groups play a crucial role in algebra and topology, facilitating the understanding of complex symmetries and geometric objects. Explore the rest of the article to deepen Your understanding of finitely presented groups and their applications.
Table of Comparison
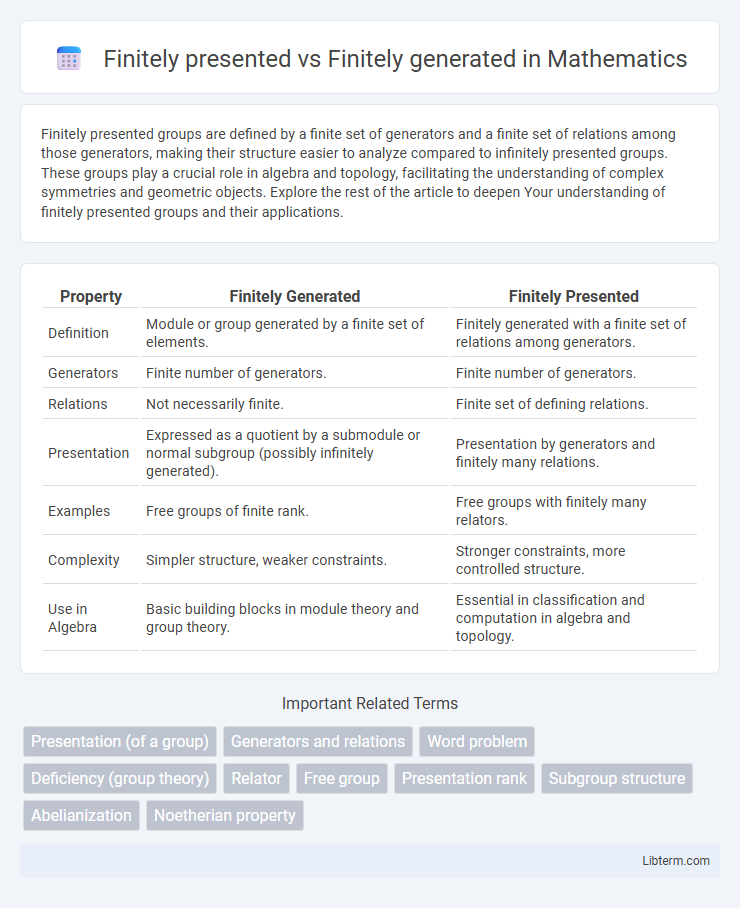
| Property | Finitely Generated | Finitely Presented |
|---|---|---|
| Definition | Module or group generated by a finite set of elements. | Finitely generated with a finite set of relations among generators. |
| Generators | Finite number of generators. | Finite number of generators. |
| Relations | Not necessarily finite. | Finite set of defining relations. |
| Presentation | Expressed as a quotient by a submodule or normal subgroup (possibly infinitely generated). | Presentation by generators and finitely many relations. |
| Examples | Free groups of finite rank. | Free groups with finitely many relators. |
| Complexity | Simpler structure, weaker constraints. | Stronger constraints, more controlled structure. |
| Use in Algebra | Basic building blocks in module theory and group theory. | Essential in classification and computation in algebra and topology. |
Introduction to Finitely Presented and Finitely Generated
Finitely generated groups are built from a finite set of elements with all group members expressed as combinations of these generators, emphasizing the minimal basis needed for construction. Finitely presented groups extend this concept by not only having a finite generating set but also a finite set of relations that fully describe the interactions and constraints among generators. Understanding finitely generated and finitely presented groups is fundamental in algebraic structures, as it connects generators and relations for comprehensive group characterization.
Defining Finitely Generated Structures
Finitely generated structures are algebraic objects, such as groups or modules, constructed from a finite set of elements whose combined operations produce the entire structure. In these structures, every element can be expressed as a combination or product of the finite generating set elements, emphasizing the generative capacity rather than the relations between them. This concept contrasts with finitely presented structures, where both a finite generating set and a finite set of defining relations are specified to completely characterize the algebraic object.
Understanding Finitely Presented Structures
Finitely presented structures are defined by a finite set of generators and a finite set of relations among those generators, providing a complete and explicit description of the object's algebraic properties. In contrast, finitely generated structures require only a finite set of generators, without necessarily having a finite set of relations, which may result in an infinite or less explicit characterization. Understanding finitely presented structures is crucial for analyzing algebraic systems like groups, rings, or modules, as it enables concrete computations and classification through a finite recursive framework.
Key Differences Between Finitely Generated and Finitely Presented
A finitely generated module or group is one where a finite set of generators produces the entire structure, while a finitely presented module or group requires both a finite generating set and a finite set of relations among those generators. The key difference lies in finitely presented structures having a finite presentation, which includes explicitly defined relations, whereas finitely generated structures do not necessarily have such finite relations specified. This distinction is crucial in algebra and group theory for understanding complexity, computability, and structural properties of algebraic objects.
Examples of Finitely Generated Groups and Modules
Finitely generated groups, such as the free group on a finite set of generators or the integer group \(\mathbb{Z}^n\), are described by a finite generating set but may have infinitely many relations. Examples of finitely presented groups include the fundamental group of a closed surface, which can be defined by a finite set of generators and relations reflecting the surface's topology. In module theory, finitely generated modules like \(\mathbb{Z}\)-modules generated by a finite number of integers contrast with finitely presented modules that require a finite number of relations, such as the cokernel of a matrix defining a module over a commutative ring.
Examples of Finitely Presented Groups and Modules
Examples of finitely presented groups include the fundamental group of a torus, given by the presentation
Algebraic Significance and Applications
Finitely generated algebraic structures have a finite set of generators from which all elements are derived through combination, crucial in constructing groups, modules, and rings. Finitely presented structures extend this concept by including a finite set of relations among the generators, enabling precise characterization and computational handling in algebraic topology, group theory, and computational algebra. These properties impact the classification of algebraic objects, decision problems, and algorithmic approaches, making finitely presented structures indispensable in understanding complexity and structural behavior.
Common Misconceptions and Pitfalls
Finitely generated modules require a finite set of generators, but finitely presented modules demand both a finite set of generators and a finite set of relations among them. A common misconception is equating finitely generated with finitely presented, overlooking that finitely presented modules offer more structural control crucial for algorithmic calculations and module classification. Ignoring this distinction can lead to errors in algebraic geometry, computational algebra, and homological algebra, where finite presentation ensures well-definedness and tractable computations.
Criteria for Identifying Finite Generation and Presentation
Finitely generated modules require a finite set of generators, meaning every element of the module can be expressed as a finite linear combination of these generators. Finitely presented modules not only have finitely many generators but also a finite set of relations among them, represented by a finite presentation matrix. Identifying finite generation involves checking whether a finite spanning set exists, while finite presentation demands verifying the finiteness of both generators and defining relations in the module structure.
Conclusion: Implications in Mathematical Structures
Finitely presented groups provide a complete characterization through a finite set of generators and relations, enabling precise control over their algebraic structure, whereas finitely generated groups require only a finite generating set without explicit relations, allowing more flexibility but less structural specificity. This distinction impacts computational group theory, as finitely presented groups facilitate algorithmic problem-solving such as the word problem, while finitely generated groups may pose undecidability challenges. Understanding these differences informs the classification and manipulation of algebraic objects in fields like topology, algebraic geometry, and combinatorial group theory.
Finitely presented Infographic
 libterm.com
libterm.com