A polyhedral complex consists of a collection of polyhedra that fit together in a structured manner, sharing faces without overlapping. These complexes are fundamental in computational geometry, topology, and combinatorics, providing a powerful framework for modeling shapes and spaces. Explore this article to understand how polyhedral complexes can enhance your grasp of geometric structures and their applications.
Table of Comparison
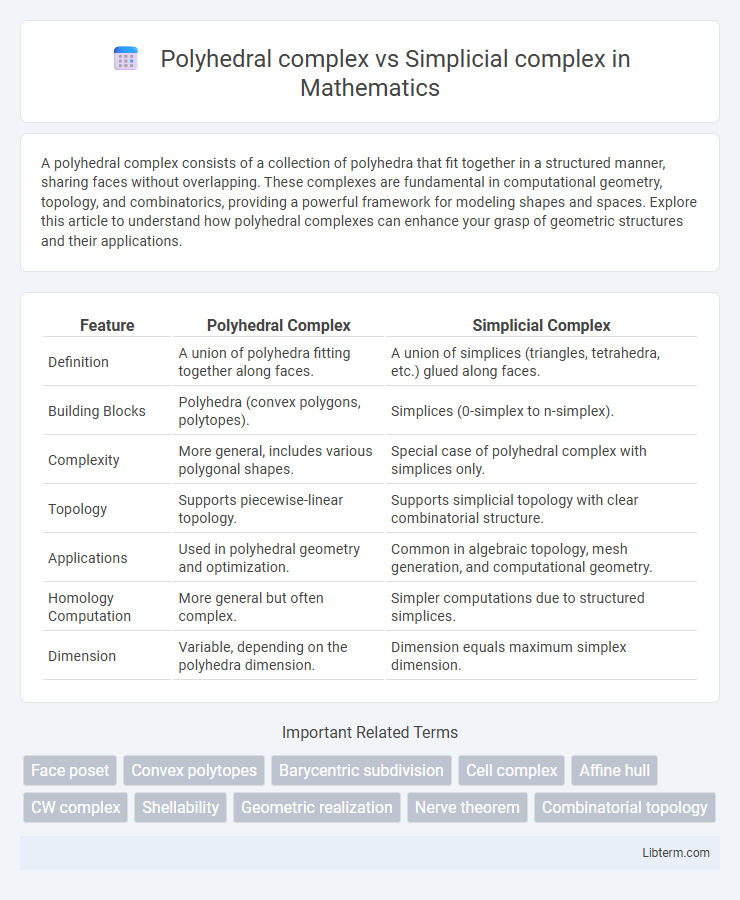
| Feature | Polyhedral Complex | Simplicial Complex |
|---|---|---|
| Definition | A union of polyhedra fitting together along faces. | A union of simplices (triangles, tetrahedra, etc.) glued along faces. |
| Building Blocks | Polyhedra (convex polygons, polytopes). | Simplices (0-simplex to n-simplex). |
| Complexity | More general, includes various polygonal shapes. | Special case of polyhedral complex with simplices only. |
| Topology | Supports piecewise-linear topology. | Supports simplicial topology with clear combinatorial structure. |
| Applications | Used in polyhedral geometry and optimization. | Common in algebraic topology, mesh generation, and computational geometry. |
| Homology Computation | More general but often complex. | Simpler computations due to structured simplices. |
| Dimension | Variable, depending on the polyhedra dimension. | Dimension equals maximum simplex dimension. |
Introduction to Polyhedral and Simplicial Complexes
Polyhedral complexes consist of polyhedra glued together along shared faces, generalizing simplicial complexes, which are made up exclusively of simplices such as triangles and tetrahedra. Simplicial complexes provide a combinatorial framework with vertices, edges, and higher-dimensional simplices, facilitating topological and geometric analysis. Polyhedral complexes expand this framework by incorporating more general convex polytopes, enabling broader applications in computational geometry and topology.
Defining Simplicial Complexes: Basics and Examples
Simplicial complexes are geometric structures composed of simplices such as points, line segments, triangles, and higher-dimensional analogs glued together along their faces. Each simplex in a simplicial complex satisfies the condition that all its faces are also included, ensuring the complex is closed under the operation of taking faces. Common examples include triangulated surfaces and polyhedra, where the simplices represent vertices, edges, and faces arranged to model the shape's combinatorial and topological properties.
Understanding Polyhedral Complexes: Structure and Types
Polyhedral complexes are geometric structures formed by gluing together polyhedra along their faces, allowing a broader range of shapes compared to simplicial complexes, which are composed exclusively of simplices like triangles or tetrahedra. The complexity of polyhedral complexes arises from the variety of polyhedral cells, including polygons, polyhedrons, and higher-dimensional polytopes, enabling the modeling of more intricate topological spaces. Understanding the structure and types of polyhedral complexes involves exploring their combinatorial properties, face lattices, and how these complexes provide a flexible framework for applications in algebraic geometry, computational topology, and optimization.
Key Differences Between Polyhedral and Simplicial Complexes
Polyhedral complexes consist of polyhedra glued together along faces, allowing cells to be general polygons or polyhedra, whereas simplicial complexes are formed exclusively from simplices, such as points, line segments, triangles, and their higher-dimensional analogs. Simplicial complexes have a combinatorial structure defined solely by simplices and their faces, ensuring every intersection between simplices is a face, while polyhedral complexes can include more complex cellular shapes with intersections that are not necessarily simplices. The key difference lies in the rigidity and simplicity of simplicial complexes versus the greater geometric flexibility and complexity afforded by polyhedral complexes.
Geometric Realizations and Representations
Polyhedral complexes generalize simplicial complexes by allowing cells to be arbitrary convex polytopes rather than restricting to simplices, leading to more flexible geometric realizations in Euclidean spaces. While simplicial complexes rely on simplices as building blocks, their geometric representation is straightforward through vertex coordinates, whereas polyhedral complexes require careful handling of polytopal faces and their intersections to maintain convexity and topology. The geometric realization of simplicial complexes ensures each simplex is embedded linearly, while polyhedral complexes accommodate a broader class of shapes, enabling richer and more complex decompositions of geometric objects.
Applications in Topology and Geometry
Polyhedral complexes, composed of convex polytopes glued together along their faces, enable the modeling of complex shapes in computational geometry and optimization, facilitating precise handling of non-simplicial cells for polytope-based algorithms. Simplicial complexes, built from simplices like triangles and tetrahedra, are fundamental in algebraic topology for persistent homology and topological data analysis, offering simpler combinatorial structures that ease computation of homology groups and Betti numbers. Both structures support mesh generation and manifold triangulation in geometric modeling, with polyhedral complexes providing greater flexibility in approximating curved spaces and simplicial complexes ensuring compatibility with standard topological invariants.
Computational Aspects: Efficiency and Usability
Polyhedral complexes offer greater flexibility in representing geometric structures by allowing polygons with arbitrary numbers of sides, which can reduce the number of cells needed and improve computational efficiency in complex modeling tasks. Simplicial complexes, composed solely of simplices such as triangles or tetrahedra, benefit from simpler algorithms and data structures that enhance usability and ease of implementation in computational topology and mesh processing. The choice between polyhedral and simplicial complexes often balances the trade-off between computational efficiency in representing complex geometries and the straightforwardness of algorithm design and software integration.
Algebraic Properties and Invariants
Polyhedral complexes generalize simplicial complexes by allowing faces with arbitrary polygonal shapes, leading to more complex algebraic structures in their associated chain complexes and homologies. Simplicial complexes exhibit well-understood algebraic invariants such as simplicial homology and cohomology, often computable via boundary operators defined on simplices. The algebraic properties of polyhedral complexes can capture richer topological information through generalized homology theories, but their invariants require more sophisticated tools due to the non-simplicial face structures.
Choosing the Right Complex for Mathematical Modeling
Choosing between a polyhedral complex and a simplicial complex depends on the complexity and dimensionality of the data to be modeled. Polyhedral complexes offer greater flexibility by incorporating cells of various polygonal shapes, making them ideal for modeling spaces with non-triangular facets or higher-dimensional polytopes. Simplicial complexes provide computational simplicity through their uniform simplex structures, which streamline algorithms in topological data analysis and mesh generation, favoring problems requiring straightforward combinatorial properties.
Future Directions and Open Problems
Future research in polyhedral complexes will address their combinatorial complexity and potential applications in high-dimensional data analysis, seeking efficient algorithms for their decomposition and reconstruction. Simplicial complexes face open problems in optimizing persistent homology computations and extending applicability to non-linear data structures while maintaining computational tractability. Advancements in both fields will likely intersect with topological data analysis, computational geometry, and machine learning, driving innovations in shape approximation and multiscale data representation.
Polyhedral complex Infographic
 libterm.com
libterm.com