The Picard group is a fundamental concept in algebraic geometry and complex analysis, representing the group of isomorphism classes of line bundles on a given algebraic variety or complex manifold. It plays a key role in understanding divisors, invertible sheaves, and the classification of algebraic varieties through its connection with the variety's geometric and topological properties. Explore the rest of the article to discover how the Picard group influences your understanding of algebraic structures and geometric classification.
Table of Comparison
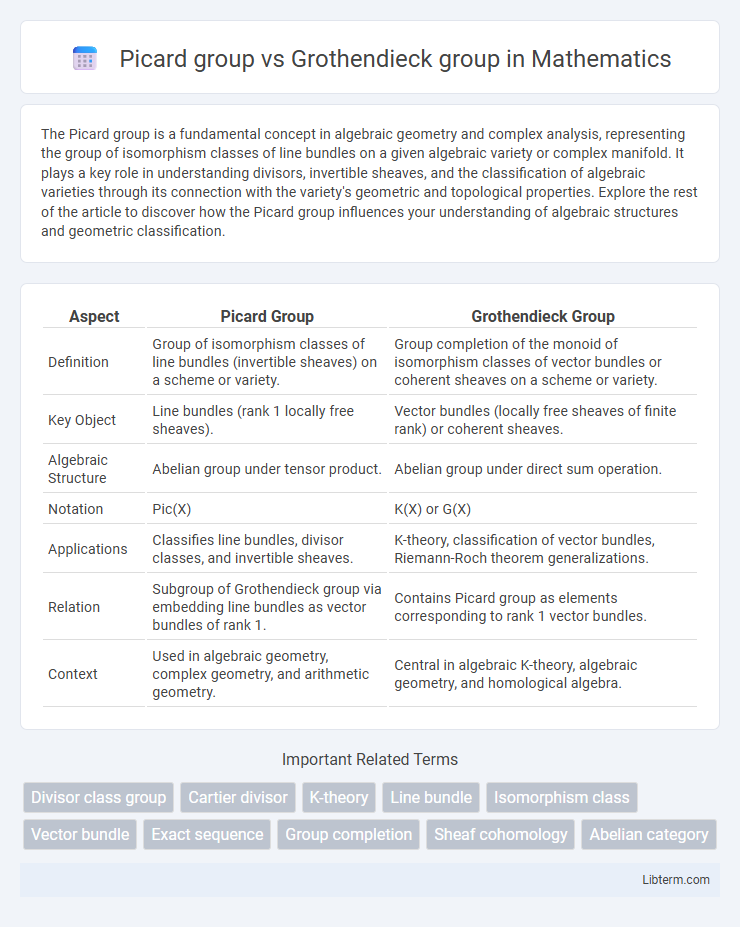
| Aspect | Picard Group | Grothendieck Group |
|---|---|---|
| Definition | Group of isomorphism classes of line bundles (invertible sheaves) on a scheme or variety. | Group completion of the monoid of isomorphism classes of vector bundles or coherent sheaves on a scheme or variety. |
| Key Object | Line bundles (rank 1 locally free sheaves). | Vector bundles (locally free sheaves of finite rank) or coherent sheaves. |
| Algebraic Structure | Abelian group under tensor product. | Abelian group under direct sum operation. |
| Notation | Pic(X) | K(X) or G(X) |
| Applications | Classifies line bundles, divisor classes, and invertible sheaves. | K-theory, classification of vector bundles, Riemann-Roch theorem generalizations. |
| Relation | Subgroup of Grothendieck group via embedding line bundles as vector bundles of rank 1. | Contains Picard group as elements corresponding to rank 1 vector bundles. |
| Context | Used in algebraic geometry, complex geometry, and arithmetic geometry. | Central in algebraic K-theory, algebraic geometry, and homological algebra. |
Introduction to the Picard Group and Grothendieck Group
The Picard group of a scheme or variety classifies isomorphism classes of line bundles, capturing essential geometric and topological information through invertible sheaves under tensor product. The Grothendieck group, often denoted K0, extends this classification to vector bundles or coherent sheaves by considering formal differences, enabling refined invariants in algebraic geometry and topology. Both groups serve as foundational tools linking geometry and algebra by encoding vector bundle data in an algebraic structure useful for intersection theory, Riemann-Roch theorems, and classification problems.
Historical Context and Motivation
The Picard group, introduced in the late 19th century by Emile Picard, originally classified line bundles on algebraic varieties, reflecting early efforts to understand divisors and class groups in algebraic geometry. The Grothendieck group, formulated by Alexander Grothendieck in the 1950s, generalized these ideas to higher-dimensional algebraic cycles and vector bundles, aiming to unify and extend concepts from K-theory and sheaf theory. This historical development was driven by the need for a comprehensive algebraic framework to systematically study vector bundles and coherent sheaves, deepening the understanding of algebraic and topological invariants.
Formal Definitions of Picard and Grothendieck Groups
The Picard group, denoted Pic(X), is defined as the group of isomorphism classes of line bundles on a scheme or variety X, with the group operation given by tensor product. The Grothendieck group, K_0(X), is constructed as the free abelian group generated by isomorphism classes of vector bundles on X, modulo the relation [E] = [E'] + [E''] for every short exact sequence 0 - E' - E - E'' - 0, encoding additive properties of vector bundles. Both groups serve as important invariants in algebraic geometry, with Pic(X) capturing the rank one component of K_0(X) and relating to divisor class groups and line bundle classification.
Key Algebraic Structures and Properties
The Picard group, formed by isomorphism classes of line bundles on a scheme or ring, is a commutative group capturing invertible sheaves under tensor product, reflecting divisor class group structures. The Grothendieck group, constructed from isomorphism classes of coherent sheaves or vector bundles, encodes additive relations via exact sequences, providing a universal group for K-theory. Both groups are pivotal in algebraic geometry and algebraic K-theory, with the Picard group emphasizing multiplicative properties of line bundles and the Grothendieck group focusing on additive invariants of sheaf categories.
Relationship Between Line Bundles and the Picard Group
The Picard group classifies isomorphism classes of line bundles on a scheme, capturing their equivalence under tensor product operations. Each element represents a distinct line bundle, making the Picard group a subgroup of the Grothendieck group of vector bundles, where only rank one bundles are considered. This relationship highlights how the Picard group serves as a refined invariant focused specifically on line bundles within the broader framework of K-theory embodied by the Grothendieck group.
Vector Bundles and the Grothendieck Group Construction
The Picard group classifies isomorphism classes of line bundles (rank one vector bundles) on a variety, capturing information about invertible sheaves under tensor product. The Grothendieck group, constructed from the monoid of isomorphism classes of vector bundles using formal differences, generalizes this by encoding vector bundles of arbitrary rank and forming a ring under direct sum and tensor product. This construction provides a powerful algebraic invariant in K-theory, connecting geometric properties of vector bundles to algebraic structures.
Functoriality and Categorical Perspectives
The Picard group, consisting of isomorphism classes of line bundles, exhibits a contravariant functoriality in schemes via pullback, making it a fundamental object in algebraic geometry. In contrast, the Grothendieck group, built from vector bundles or coherent sheaves, is functorial with respect to exact sequences and behaves covariantly under pushforward in suitable settings, reflecting its deep ties to K-theory. From a categorical viewpoint, the Picard group arises as the group of invertible objects in a symmetric monoidal category, whereas the Grothendieck group is a universal recipient of Euler characteristics in exact categories, highlighting distinct but complementary structural roles.
Comparison: Additivity and Tensor Product Structures
The Picard group classifies isomorphism classes of line bundles under the tensor product operation, exhibiting a strictly commutative group structure driven by the tensor product of invertible sheaves. In contrast, the Grothendieck group, constructed from isomorphism classes of vector bundles or coherent sheaves via formal differences, carries an additive group structure reflecting exact sequences, and its tensor product operation induces a ring structure rather than just a group. The Picard group can be viewed as a subgroup of the Grothendieck group focusing on rank-one vector bundles, capturing multiplicative features, while the Grothendieck group encodes additive information of all vector bundles, making the interplay between additivity and multiplicativity central to their comparative study.
Examples and Applications in Algebraic Geometry
The Picard group classifies line bundles on algebraic varieties, with examples including the Picard group of a smooth projective curve is isomorphic to its Jacobian variety, illustrating connections to divisor class groups. The Grothendieck group, constructed from coherent sheaves, exemplifies a broader invariant capturing vector bundles and their extensions, and its application in algebraic geometry is crucial for K-theory computations on schemes. Both groups play pivotal roles in studying vector bundles, divisors, and Chern classes, with the Picard group often appearing in classification problems while the Grothendieck group facilitates understanding of more complex sheaf-theoretic and K-theoretic phenomena.
Summary of Differences and Interconnections
The Picard group classifies isomorphism classes of line bundles on a scheme or variety, capturing invertible sheaves under tensor product, while the Grothendieck group, often denoted K_0, generalizes this by encoding vector bundles or coherent sheaves through formal differences, reflecting algebraic K-theory structure. The Picard group embeds naturally into the Grothendieck group, identifying line bundles as classes of rank one vector bundles within K_0, linking geometric aspects of divisors with algebraic invariants. Interconnections between these groups arise in cohomological and intersection-theoretic contexts, with the Picard group influencing the structure of K_0 via the first Chern class homomorphism and determinant maps.
Picard group Infographic
 libterm.com
libterm.com