An Abelian group is a fundamental algebraic structure characterized by a set equipped with an associative binary operation that is commutative, meaning the order of operation does not affect the outcome. Each element has an inverse, and there exists an identity element within the group satisfying specific axioms, making Abelian groups essential in various branches of mathematics and physics. Explore the rest of the article to deepen your understanding of Abelian groups and their applications.
Table of Comparison
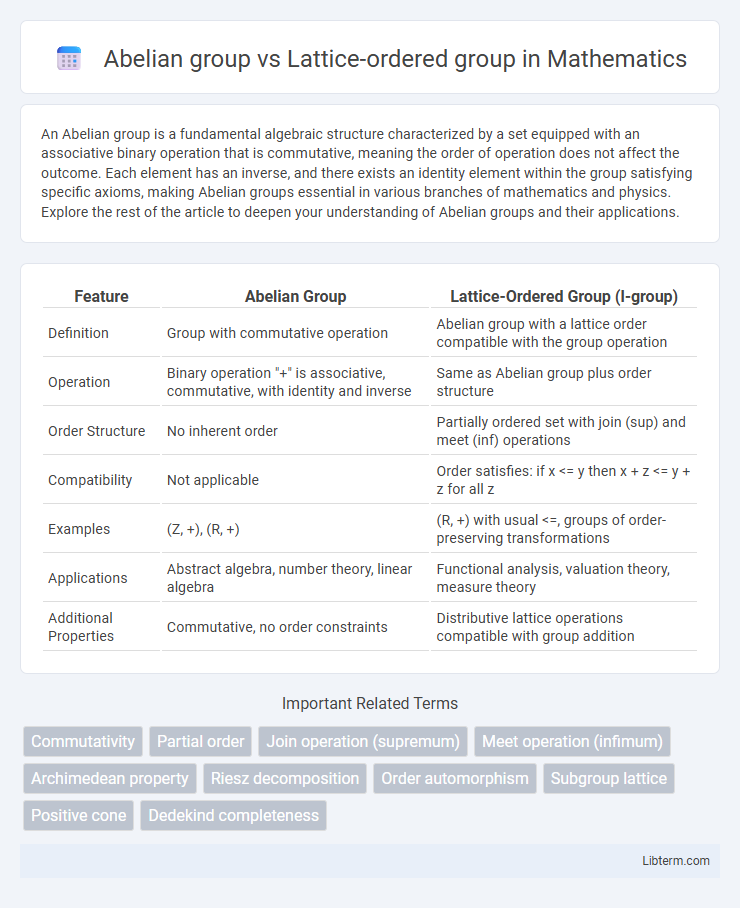
| Feature | Abelian Group | Lattice-Ordered Group (l-group) |
|---|---|---|
| Definition | Group with commutative operation | Abelian group with a lattice order compatible with the group operation |
| Operation | Binary operation "+" is associative, commutative, with identity and inverse | Same as Abelian group plus order structure |
| Order Structure | No inherent order | Partially ordered set with join (sup) and meet (inf) operations |
| Compatibility | Not applicable | Order satisfies: if x <= y then x + z <= y + z for all z |
| Examples | (Z, +), (R, +) | (R, +) with usual <=, groups of order-preserving transformations |
| Applications | Abstract algebra, number theory, linear algebra | Functional analysis, valuation theory, measure theory |
| Additional Properties | Commutative, no order constraints | Distributive lattice operations compatible with group addition |
Introduction to Abelian Groups
Abelian groups are algebraic structures characterized by commutative group operations where the group operation satisfies the commutative property, meaning for any elements a and b, a + b = b + a. Lattice-ordered groups extend Abelian groups by integrating a lattice order compatible with the group operation, allowing elements to be compared with respect to an order relation while preserving group structure. Understanding Abelian groups provides a foundational basis for studying lattice-ordered groups, emphasizing commutativity and group axioms without additional order constraints.
Understanding Lattice-Ordered Groups
Lattice-ordered groups, or l-groups, extend Abelian groups by incorporating a lattice structure where every pair of elements has a well-defined supremum and infimum, enabling order-theoretic analysis alongside group operations. These groups maintain commutativity in the group operation and satisfy compatibility conditions between the group order and lattice operations, ensuring the order is translation-invariant. Understanding lattice-ordered groups involves studying their algebraic and order properties, which apply to areas such as functional analysis and the theory of Riesz spaces.
Fundamental Properties of Abelian Groups
Abelian groups exhibit commutativity in their group operation, defined by the equation a * b = b * a for all elements a and b, ensuring a symmetrical algebraic structure. These groups satisfy the fundamental properties of associativity, the existence of identity elements, and inverses, making them a central concept in abstract algebra. Unlike lattice-ordered groups, Abelian groups do not inherently possess order or lattice structures, focusing purely on the algebraic properties of commutative group operations.
Core Characteristics of Lattice-Ordered Groups
Lattice-ordered groups (l-groups) combine group theory with lattice theory, featuring elements equipped with a partial order that is compatible with the group operation, allowing the definition of meet and join for every pair of elements. Core characteristics include the existence of a lattice structure where every two elements have a least upper bound and greatest lower bound, and group operations preserving these order relations. Unlike Abelian groups, l-groups emphasize order-theoretic properties alongside algebraic ones, enabling applications in areas such as functional analysis and ordered algebraic systems.
Key Differences Between Abelian and Lattice-Ordered Groups
Abelian groups are algebraic structures characterized by commutative group operations where every element has an inverse, while lattice-ordered groups (l-groups) combine group theory with lattice theory, allowing elements to be partially ordered with defined meet and join operations. Abelian groups emphasize commutativity and invertibility, whereas lattice-ordered groups integrate order relations compatible with group operations, making them suitable for applications in ordered algebraic systems. The critical difference lies in lattice-ordered groups possessing both group and lattice structures simultaneously, enabling the study of order-theoretic properties alongside classical group properties.
Structural Similarities in Group Theory
Abelian groups and lattice-ordered groups (l-groups) share a core structural similarity in that both possess an underlying group operation that is associative, commutative in the case of Abelian groups, and compatible with a partial order in l-groups. The lattice order in l-groups extends the algebraic structure of Abelian groups by introducing meet and join operations that satisfy lattice axioms, enabling a richer interplay between order and algebraic operations. Both structures allow the decomposition of elements and the study of homomorphisms preserving their respective group and order-theoretic properties, making them fundamental in the study of ordered algebraic systems.
Examples of Abelian Groups and Lattice-Ordered Groups
The group of integers under addition, \((\mathbb{Z}, +)\), serves as a classic example of an Abelian group where the operation is commutative. The group of real numbers with usual addition equipped with the order induced by the usual <= relation forms a lattice-ordered group (l-group) with the lattice operations given by pointwise minimum and maximum. Finite cyclic groups like \(\mathbb{Z}/n\mathbb{Z}\) exemplify Abelian groups without a natural lattice order, while free Abelian lattice-ordered groups generated by finitely many elements illustrate nontrivial structures where the group and lattice orders coexist.
Applications in Mathematics and Beyond
Abelian groups provide a fundamental algebraic framework used in number theory, cryptography, and topology due to their commutative property, facilitating solutions in homology and group cohomology. Lattice-ordered groups extend Abelian group structure by incorporating a lattice order compatible with group operations, enabling applications in functional analysis, decision theory, and mathematical economics, particularly in optimization and preference modeling. The interplay between algebraic and order-theoretic properties in lattice-ordered groups unlocks advanced techniques in measure theory and theoretical computer science, enriching both pure and applied mathematical disciplines.
Algebraic Structures: Comparisons and Contrasts
Abelian groups are algebraic structures characterized by a commutative binary operation satisfying closure, associativity, identity, and invertibility, whereas lattice-ordered groups (l-groups) combine group operations with a lattice order compatible with group addition. In l-groups, every pair of elements has a well-defined meet and join, integrating both algebraic and order-theoretic properties, which contrasts with the purely group-theoretic nature of Abelian groups. The interplay between group operations and order in lattice-ordered groups provides a richer framework for studying ordered algebraic systems beyond the scope of Abelian groups.
Concluding Insights on Group Types
Abelian groups exhibit commutative properties where the group operation is symmetric, simplifying their algebraic structure compared to lattice-ordered groups which incorporate a partial order compatible with the group operation, forming a richer, more complex hierarchy. Lattice-ordered groups enable the definition of meets and joins for any two elements, blending group theory with lattice theory and facilitating studies in ordered algebraic systems and functional analysis. Understanding these distinctions provides critical insights into algebraic structures, highlighting how commutativity and order interplay influence the applicability of groups in mathematical and applied contexts.
Abelian group Infographic
 libterm.com
libterm.com