Total order is a fundamental concept in mathematics and computer science, referring to a binary relation that arranges elements in a linear sequence where every pair of elements is comparable. This ensures that for any two elements, one is always greater than or equal to the other, enabling efficient sorting and decision-making algorithms. Discover how total order impacts various applications and why understanding it is crucial for optimizing Your data structures by reading the full article.
Table of Comparison
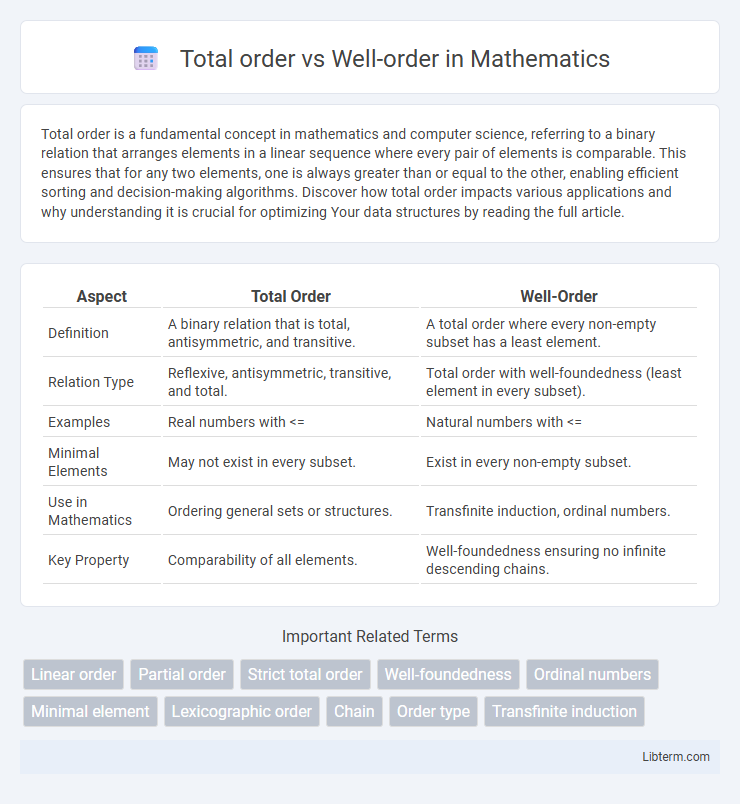
| Aspect | Total Order | Well-Order |
|---|---|---|
| Definition | A binary relation that is total, antisymmetric, and transitive. | A total order where every non-empty subset has a least element. |
| Relation Type | Reflexive, antisymmetric, transitive, and total. | Total order with well-foundedness (least element in every subset). |
| Examples | Real numbers with <= | Natural numbers with <= |
| Minimal Elements | May not exist in every subset. | Exist in every non-empty subset. |
| Use in Mathematics | Ordering general sets or structures. | Transfinite induction, ordinal numbers. |
| Key Property | Comparability of all elements. | Well-foundedness ensuring no infinite descending chains. |
Introduction to Order Relations
Total order is a binary relation on a set where every pair of elements is comparable, meaning for any two elements a and b, either a <= b or b <= a holds. Well-order extends total order by requiring every non-empty subset to have a least element, ensuring no infinite descending sequences exist. Both concepts are foundational in set theory and order theory, with total orders used in sorting and well-orders crucial for transfinite induction.
Defining Total Order
A total order is a binary relation on a set that is transitive, antisymmetric, and total, meaning every pair of elements is comparable under the relation. In contrast to well-orders, total orders do not require every non-empty subset to have a least element. Total orders provide a foundation for sorting and sequencing operations, essential in mathematics and computer science.
Understanding Well-Order
A well-order is a total order with the added condition that every non-empty subset has a least element, ensuring no infinite descending chains exist. Unlike a generic total order, which only requires comparability between any two elements, a well-order enforces a strict foundation useful in transfinite induction and ordinal number theory. Understanding well-orders involves recognizing their role in structuring sets for proofs and hierarchies where minimal elements are guaranteed, facilitating algorithmic and theoretical applications in mathematics and computer science.
Key Differences between Total Order and Well-Order
A total order is a binary relation on a set that is antisymmetric, transitive, and total, meaning every pair of elements is comparable, while a well-order is a total order with the additional condition that every non-empty subset has a least element. Total orders include familiar structures like the usual ordering of real numbers, whereas well-orders are crucial in set theory and ordinal analysis due to their minimal element property. The key difference lies in the well-order's guarantee of minimal elements, enabling transfinite induction, which is not required or ensured in total orders.
Examples of Total Orders
A total order is a binary relation on a set where every pair of elements is comparable, such as the usual order on real numbers (<=) or the alphabetical order of words in a dictionary. For instance, the natural numbers with the standard less-than-or-equal relation (<=) form a total order, as do the integers, rational numbers, and lexicographic order on tuples. These examples illustrate that total orders allow linear ranking of elements, but unlike well-orders, total orders may have infinite descending chains.
Examples of Well-Orders
The set of natural numbers \(\mathbb{N}\) under the usual less-than relation \((<)\) is a classic example of a well-order, where every non-empty subset has a least element. Ordinal numbers, such as \(\omega\), extend natural numbers and also form well-orders, including infinite sequences with order types beyond \(\mathbb{N}\). In contrast, total orders like the real numbers \(\mathbb{R}\) with standard ordering are not well-orders since subsets like the open interval \((0,1)\) lack a least element.
Applications of Total Order
Total orders provide a foundational framework for sorting algorithms, enabling efficient data organization and retrieval in computer science applications such as databases and search engines. They are essential in scheduling problems where tasks must be performed in a linear sequence to satisfy precedence constraints. In mathematics and economics, total orders facilitate decision making by establishing a clear preference ranking among alternatives, ensuring consistency and comparability.
Applications of Well-Order
Well-order relations are crucial in set theory and logic, especially for proving principles like transfinite induction and recursion across ordinals. They enable the classification of ordinal numbers, which underpin foundational concepts in mathematics and computer science, including algorithm termination proofs and type theory. Applications extend to decision-making processes in economics and formal verification, where well-ordered structures ensure completeness and consistency.
Importance in Set Theory and Mathematics
Total order ensures every pair of elements in a set is comparable, providing a complete framework for structuring data and enabling proofs involving sequences and optimization. Well-order extends total order by requiring every non-empty subset to have a least element, a critical property for transfinite induction and ordinal number theory in set theory. The distinction between these orders underpins foundational results in mathematics, such as the well-ordering theorem and the development of ordinal and cardinal numbers.
Summary and Comparison of Total Order vs Well-Order
A total order is a binary relation on a set where every pair of elements is comparable, ensuring a linear or complete ordering, while a well-order extends this by requiring every non-empty subset to have a least element. Total orders support sequences where elements can be arranged linearly, whereas well-orders guarantee the existence of a minimal element, critical for transfinite induction and ordinal analysis. The key distinction lies in well-orders enabling structured minimality constraints, making them fundamental in set theory compared to general total orders.
Total order Infographic
 libterm.com
libterm.com