Convergence in probability describes a sequence of random variables that become increasingly close to a fixed value as the sample size grows. This concept is fundamental in statistics and probability theory, ensuring that estimators reliably approximate the true parameter. Explore the full article to understand how convergence in probability impacts your statistical analyses.
Table of Comparison
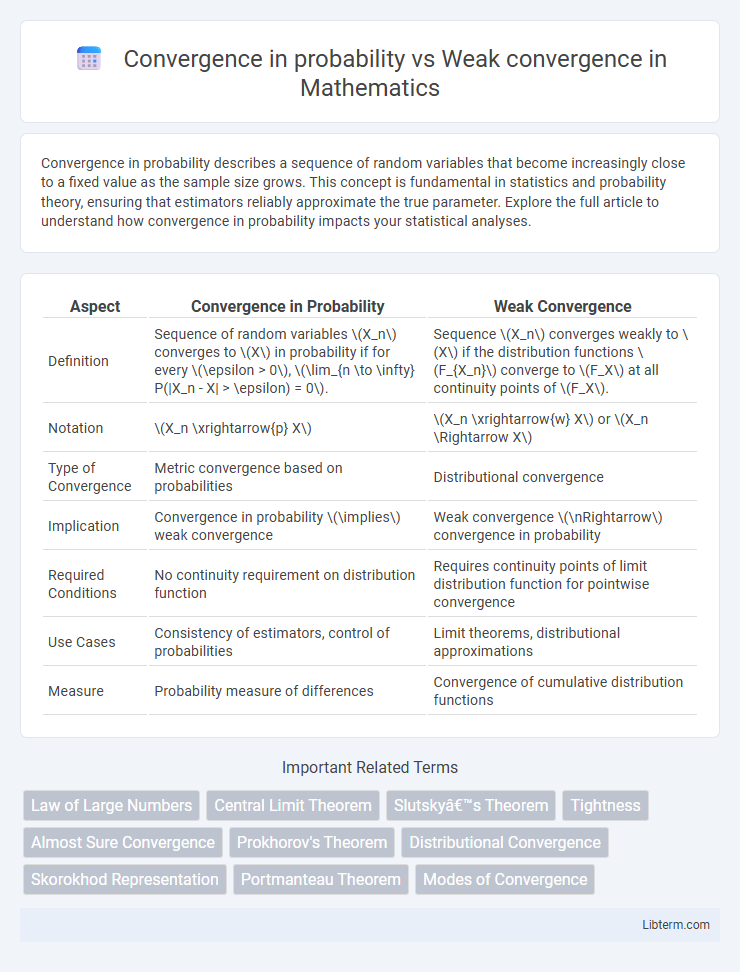
| Aspect | Convergence in Probability | Weak Convergence |
|---|---|---|
| Definition | Sequence of random variables \(X_n\) converges to \(X\) in probability if for every \(\epsilon > 0\), \(\lim_{n \to \infty} P(|X_n - X| > \epsilon) = 0\). | Sequence \(X_n\) converges weakly to \(X\) if the distribution functions \(F_{X_n}\) converge to \(F_X\) at all continuity points of \(F_X\). |
| Notation | \(X_n \xrightarrow{p} X\) | \(X_n \xrightarrow{w} X\) or \(X_n \Rightarrow X\) |
| Type of Convergence | Metric convergence based on probabilities | Distributional convergence |
| Implication | Convergence in probability \(\implies\) weak convergence | Weak convergence \(\nRightarrow\) convergence in probability |
| Required Conditions | No continuity requirement on distribution function | Requires continuity points of limit distribution function for pointwise convergence |
| Use Cases | Consistency of estimators, control of probabilities | Limit theorems, distributional approximations |
| Measure | Probability measure of differences | Convergence of cumulative distribution functions |
Introduction to Convergence in Probability and Weak Convergence
Convergence in probability describes a sequence of random variables approaching a fixed value such that for any positive threshold, the probability that the variables deviate from that value beyond the threshold tends to zero as the sequence progresses. Weak convergence, also known as convergence in distribution, occurs when the cumulative distribution functions of the random variables converge pointwise to the cumulative distribution function of the target variable at all continuity points. Both types of convergence play essential roles in probability theory and statistical inference, with convergence in probability implying weak convergence under certain conditions but not vice versa.
Fundamental Definitions
Convergence in probability occurs when the probability that a sequence of random variables deviates from a limiting variable by more than any positive number approaches zero as the sequence progresses. Weak convergence, or convergence in distribution, happens when the cumulative distribution functions of random variables converge to the cumulative distribution function of the limiting variable at all continuity points. The key difference lies in the convergence criteria: convergence in probability implies the random variables increasingly cluster near the limit, while weak convergence concerns the convergence of distribution functions rather than the random variables themselves.
Mathematical Formulations
Convergence in probability is defined as a sequence of random variables \(X_n\) satisfying \(\forall \epsilon > 0, \lim_{n \to \infty} P(|X_n - X| > \epsilon) = 0\), where \(X\) is a random variable, emphasizing pointwise probability bounds. Weak convergence, or convergence in distribution, requires that the cumulative distribution functions satisfy \(\lim_{n \to \infty} F_{X_n}(t) = F_X(t)\) at all continuity points \(t\) of \(F_X\), focusing on the convergence of distribution functions rather than realizations. The key distinction lies in convergence in probability implying convergence in distribution, but not vice versa, reflecting different degrees of closeness between sequences of random variables in probability theory.
Key Differences Between the Two Convergences
Convergence in probability occurs when the probability that a sequence of random variables deviates from a limiting variable by more than any positive number goes to zero, emphasizing pointwise closeness. Weak convergence, or convergence in distribution, requires the sequence's cumulative distribution functions to converge at all continuity points of the limiting distribution function, focusing on distributional behavior rather than individual outcomes. Key differences include that convergence in probability implies weak convergence, but weak convergence does not guarantee convergence in probability, highlighting their distinct roles in probability theory and statistical inference.
Examples Illustrating Convergence in Probability
Convergence in probability is demonstrated when a sequence of random variables \(X_n\) satisfies \(P(|X_n - X| > \epsilon) \to 0\) for every \(\epsilon > 0\), as seen in the example where \(X_n = \frac{1}{n}Z\) with \(Z\) bounded; this implies \(X_n\) converges in probability to 0. Unlike weak convergence, which relies on the convergence of distribution functions, convergence in probability ensures the random variables themselves become arbitrarily close with high probability. Examples such as the sample mean \(\bar{X}_n\) converging to the expected value \(\mu\) in the Law of Large Numbers illustrate this concept effectively.
Examples Demonstrating Weak Convergence
Weak convergence, also known as convergence in distribution, occurs when the distribution functions of a sequence of random variables converge to the distribution function of a limiting variable, without requiring pointwise convergence. For example, the Central Limit Theorem demonstrates weak convergence as the normalized sum of independent, identically distributed variables converges in distribution to a normal random variable. Another example is the convergence of the empirical distribution function to the true cumulative distribution function, illustrating weak convergence in the context of statistical estimation.
Relationships and Hierarchies
Convergence in probability implies weak convergence, establishing a hierarchical relationship where convergence in probability is a stronger condition than weak convergence. Weak convergence, also known as convergence in distribution, describes the convergence of distribution functions, while convergence in probability ensures the random variables themselves are close with high probability. This hierarchy highlights that every sequence converging in probability also converges weakly, but not every weakly convergent sequence converges in probability.
Common Applications in Probability Theory
Convergence in probability is widely used in statistical estimation to guarantee that estimators approach the true parameter value as sample size increases. Weak convergence, or convergence in distribution, plays a crucial role in the central limit theorem and the asymptotic behavior of stochastic processes. Both types of convergence are foundational in the theory of large sample properties and in the analysis of random variable sequences in probability theory.
Theoretical Implications for Statistical Inference
Convergence in probability ensures that estimates become arbitrarily close to the true parameter with high probability, providing strong consistency essential for reliable point estimation. Weak convergence, or convergence in distribution, characterizes the limiting behavior of normalized sums or statistics, underpinning the validity of asymptotic approximations such as the Central Limit Theorem. Understanding the distinction informs the choice of inference methods, where convergence in probability supports confidence in estimator accuracy, while weak convergence justifies the use of limit distributions for hypothesis testing and constructing confidence intervals.
Summary and Comparative Insights
Convergence in probability occurs when the probability that a sequence of random variables differs from a limit by more than any positive epsilon approaches zero, emphasizing pointwise behavior. Weak convergence, also known as convergence in distribution, involves the convergence of cumulative distribution functions at all continuity points of the limit distribution, focusing on the distributional shape rather than individual outcomes. While convergence in probability implies weak convergence, the converse is not true, highlighting that convergence in probability is a stronger form of convergence used for almost sure approximation in stochastic analysis.
Convergence in probability Infographic
 libterm.com
libterm.com