A bundle offers a convenient way to combine multiple products or services into one attractive package, often at a discounted price. This approach not only saves you money but also simplifies the purchasing process, making it easier to access everything you need in a single transaction. Discover how bundling can maximize your value by reading the full article.
Table of Comparison
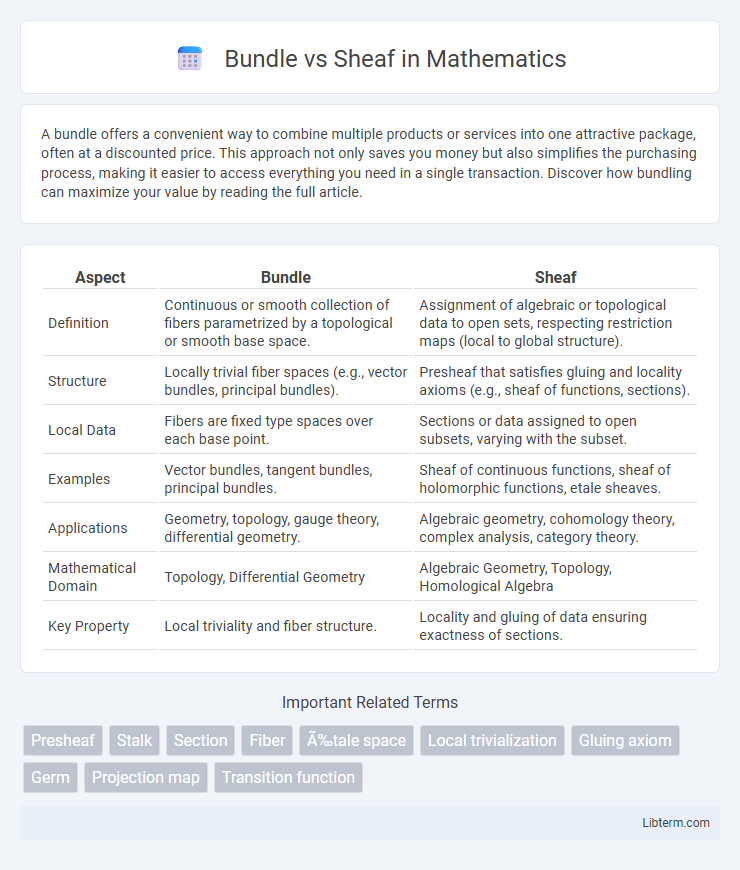
| Aspect | Bundle | Sheaf |
|---|---|---|
| Definition | Continuous or smooth collection of fibers parametrized by a topological or smooth base space. | Assignment of algebraic or topological data to open sets, respecting restriction maps (local to global structure). |
| Structure | Locally trivial fiber spaces (e.g., vector bundles, principal bundles). | Presheaf that satisfies gluing and locality axioms (e.g., sheaf of functions, sections). |
| Local Data | Fibers are fixed type spaces over each base point. | Sections or data assigned to open subsets, varying with the subset. |
| Examples | Vector bundles, tangent bundles, principal bundles. | Sheaf of continuous functions, sheaf of holomorphic functions, etale sheaves. |
| Applications | Geometry, topology, gauge theory, differential geometry. | Algebraic geometry, cohomology theory, complex analysis, category theory. |
| Mathematical Domain | Topology, Differential Geometry | Algebraic Geometry, Topology, Homological Algebra |
| Key Property | Local triviality and fiber structure. | Locality and gluing of data ensuring exactness of sections. |
Introduction: Understanding Bundle and Sheaf
A bundle is a mathematical structure consisting of a base space and a fiber attached smoothly at every point, enabling continuous local trivialization, commonly seen in vector bundles and fiber bundles. A sheaf, in contrast, systematically associates algebraic or topological data to open sets of a topological space, facilitating the localization and gluing of sections or functions. Understanding the distinction hinges on bundles focusing on geometric projections and fibers, while sheaves emphasize the organization and restriction of data over varying subsets.
Mathematical Foundations of Bundles
Bundles in mathematics are structured as a topological space resembling a product space locally, enabling the study of continuous projections between spaces, while sheaves generalize this concept by systematically assigning algebraic structures or sets to open subsets of a topological space, reflecting local-to-global properties. The mathematical foundations of bundles rely on fiber bundles, consisting of a total space, base space, projection map, and a typical fiber, supporting the formulation of principal and vector bundles fundamental in differential geometry and topology. Sheaf theory extends these ideas by encoding local data with restriction maps, allowing advanced applications in cohomology and algebraic geometry, where bundles provide the geometric scaffold for sheaf constructions.
Defining Sheaves in Topology
Sheaves in topology generalize bundles by encoding local data and their compatible gluing across open sets of a topological space, formalized as a presheaf satisfying the sheaf axioms of locality and gluing. Unlike fiber bundles characterized by continuous projections and locally trivial fibers, sheaves capture variable algebraic or geometric structures such as functions, sections, or modules on open neighborhoods. The key defining feature of a sheaf is its ability to reconcile local consistency with global coherence, making it essential for cohomological methods and modern algebraic geometry.
Key Differences Between Bundle and Sheaf
Bundles consist of a topological space (total space) with a projection map onto a base space, where each fiber is a fixed type of mathematical object like a vector space, emphasizing local triviality. Sheaves assign algebraic structures or sets to open subsets of a topological space, along with restriction maps that satisfy gluing and locality conditions, focusing on local data and its consistency across overlaps. The key difference lies in bundles capturing globally structured fibered spaces, while sheaves encode local algebraic information systematically over open sets.
Applications of Bundles in Geometry
Bundles play a crucial role in differential geometry by providing a framework to study fibered structures such as tangent bundles and vector bundles, which facilitate the examination of smooth manifolds and their properties. Applications include the formulation of curvature, connections, and characteristic classes that are essential in understanding geometric and topological invariants. These structures enable the study of gauge theory, complex geometry, and global analysis by offering tools to analyze local-to-global phenomena in a rigorous manner.
Sheaf Theory and Its Significance
Sheaf theory provides a powerful framework for systematically tracking local data attached to open subsets of a topological space and their consistent gluing across overlaps, crucial in fields like algebraic geometry, differential topology, and complex analysis. Unlike bundles, which primarily encode geometric data varying smoothly over a base space, sheaves generalize this concept by handling more abstract data types, including functions, rings, and modules, with applications in cohomology and the study of singularities. The significance of sheaf theory lies in its ability to unify various mathematical structures and facilitate the analysis of global properties through local-to-global principles.
Bundle vs Sheaf: Structural Comparison
Bundles consist of a continuous family of spaces parameterized by a base space, where each fiber is isomorphic and locally trivial, while sheaves systematically assign algebraic or topological data to open subsets, capturing local-to-global properties. Structurally, bundles emphasize fiberwise homogeneity and local triviality equipped with transition functions, whereas sheaves focus on the compatibility of sections over varying open sets and the gluing axioms. The key difference lies in bundles modeling geometric objects like vector bundles or principal bundles, whereas sheaves generalize to data organization frameworks suitable for cohomological methods and local data reconstruction.
Real-world Examples of Bundles and Sheaves
Bundles are exemplified by vector bundles such as the tangent bundle in differential geometry, representing the collection of tangent spaces smoothly varying over a manifold. Sheaves model data assignment systems like the sheaf of continuous functions on a topological space, capturing local-to-global properties. Real-world applications include fiber optic cables as physical analogs of bundles and database schemas aligned with sheaf theory principles ensuring consistency across distributed datasets.
Advantages and Limitations: Bundle vs Sheaf
Bundles provide a straightforward framework for modeling locally trivial fiber spaces with well-defined projection maps, enabling easier visualization and manipulation in differential geometry. Sheaves offer greater flexibility by encoding local data and their consistency conditions, making them powerful tools for handling complex, variable topological or algebraic structures. However, bundles may be limited in capturing intricate local-to-global relationships, whereas sheaves require more abstract categorical techniques, potentially complicating concrete computations.
Conclusion: Choosing Between Bundle and Sheaf
Choosing between a bundle and a sheaf depends on the specific mathematical context and application, with bundles providing a structured approach to fiber spaces over a base manifold, ideal for differential geometry and topology. Sheaves offer greater flexibility in managing local data consistent across open sets, making them essential in algebraic geometry and complex analysis. The decision hinges on whether the problem requires the concrete global topological framework of bundles or the local-to-global data coherence emphasized in sheaf theory.
Bundle Infographic
 libterm.com
libterm.com