A cell complex is a topological space constructed by gluing cells such as points, lines, disks, and higher-dimensional analogs in a structured way to study their shape and properties. These complexes serve as fundamental tools in algebraic topology for analyzing spaces through their decomposition into simpler pieces. Explore the rest of the article to learn how cell complexes provide powerful methods for understanding complex geometrical structures.
Table of Comparison
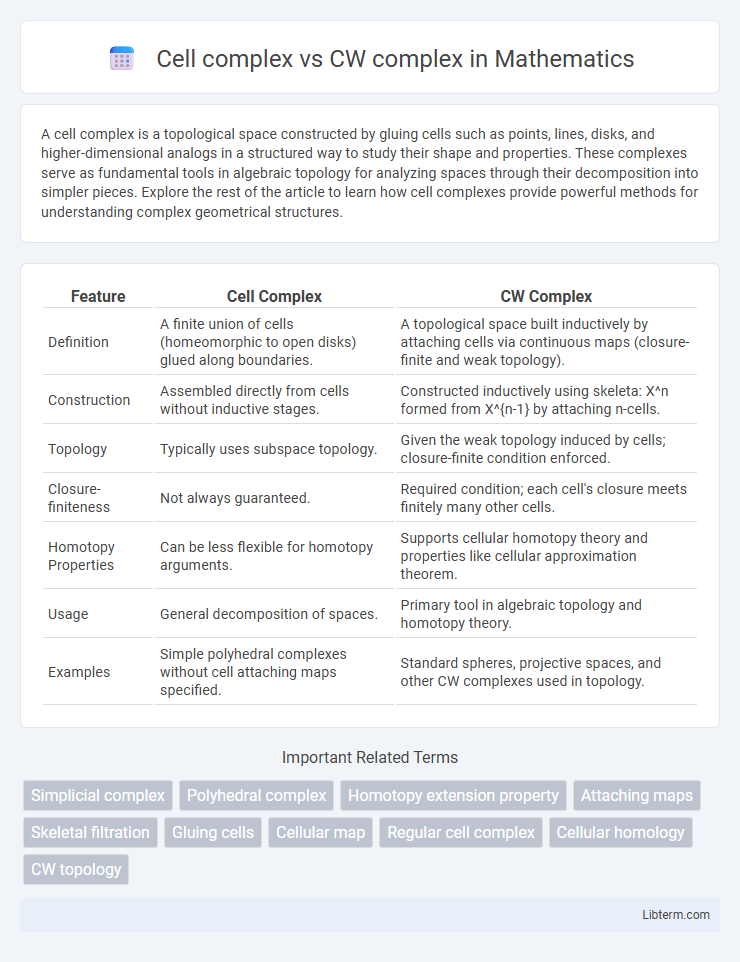
| Feature | Cell Complex | CW Complex |
|---|---|---|
| Definition | A finite union of cells (homeomorphic to open disks) glued along boundaries. | A topological space built inductively by attaching cells via continuous maps (closure-finite and weak topology). |
| Construction | Assembled directly from cells without inductive stages. | Constructed inductively using skeleta: X^n formed from X^{n-1} by attaching n-cells. |
| Topology | Typically uses subspace topology. | Given the weak topology induced by cells; closure-finite condition enforced. |
| Closure-finiteness | Not always guaranteed. | Required condition; each cell's closure meets finitely many other cells. |
| Homotopy Properties | Can be less flexible for homotopy arguments. | Supports cellular homotopy theory and properties like cellular approximation theorem. |
| Usage | General decomposition of spaces. | Primary tool in algebraic topology and homotopy theory. |
| Examples | Simple polyhedral complexes without cell attaching maps specified. | Standard spheres, projective spaces, and other CW complexes used in topology. |
Introduction to Cell Complexes
A cell complex is a topological space constructed by gluing cells of various dimensions, such as points, line segments, disks, and higher-dimensional analogs, in a structured manner. CW complexes are a specialized type of cell complex defined by the closure-finiteness and weak topology conditions, ensuring more manageable and combinatorial properties. CW complexes are fundamental in algebraic topology due to their tractable homotopy and homology theories, making them a preferred framework over general cell complexes.
Overview of CW Complexes
CW complexes are topological spaces constructed by inductively attaching cells of increasing dimension via continuous maps from their boundaries, providing a flexible framework for analyzing complex shapes in algebraic topology. Each stage in building a CW complex involves gluing n-dimensional disks (cells) to the (n-1)-skeleton, ensuring well-behaved closure properties and enabling computation of homotopy and homology groups. This cellular structure generalizes cell complexes by emphasizing closure-finiteness and weak topology, facilitating powerful topological invariants and homotopy equivalences.
Defining Cell Complexes: Key Concepts
A cell complex is a topological space constructed by gluing cells (balls of various dimensions) together via continuous attaching maps, forming a structured assembly of 0-cells, 1-cells, 2-cells, and higher-dimensional cells. A CW complex refines this concept by adhering to closure-finiteness and weak topology conditions, where cells are attached inductively in increasing dimension, ensuring each cell intersects the complex's skeleton in a controlled manner. The key concepts defining cell complexes involve the dimension, attaching maps, and the topological properties that enable analysis of homotopy and homology within algebraic topology.
The Construction of CW Complexes
CW complexes are constructed by inductively attaching cells of increasing dimension via continuous maps from the boundary spheres into the existing complex, ensuring a closure-finite and weak topology structure. Unlike general cell complexes, CW complexes impose specific attaching maps that provide well-behaved topological properties essential for homotopy theory and algebraic topology. This construction enables a systematic buildup from 0-cells (points) to higher-dimensional cells, creating spaces that are easier to analyze and manipulate in topological studies.
Topological Properties: Cell vs. CW Complex
Cell complexes are built by attaching cells of various dimensions using continuous maps, but they may lack the closure-finiteness and weak topology conditions that characterize CW complexes. CW complexes ensure well-behaved topological properties such as closure-finiteness, meaning each cell's closure intersects only finitely many cells, and the weak topology where a set is closed if and only if its intersection with each cell closure is closed. These properties make CW complexes particularly suitable for homotopy and homology studies, providing a more structured and manageable framework compared to general cell complexes.
Homotopy and Homology in Both Complexes
Cell complexes and CW complexes serve as foundational tools in algebraic topology for analyzing spaces through homotopy and homology groups. CW complexes generalize cell complexes by allowing cells to be attached via characteristic maps that meet closure-finiteness and weak topology conditions, facilitating more flexible homotopy equivalences and enabling calculation of homology using cellular chains. Both complexes support the computation of homology and homotopy groups, but CW complexes offer more refined control in constructing homotopy type invariants and cellular homology due to their structured inductive cell attachment.
Examples: Cell Complexes and CW Complexes
Cell complexes include structures like simplicial complexes formed by gluing simplices along faces, while CW complexes expand this concept by attaching cells of varying dimensions using characteristic maps, enabling more flexible topological constructions. For example, a 2-dimensional torus can be realized as a cell complex by identifying edges of polygons or as a CW complex by attaching one 0-cell, two 1-cells, and one 2-cell with specified attaching maps. The CW complex framework supports more generality in cell attachments, allowing for complex spaces such as projective spaces and wedge sums to be built systematically.
Advantages of CW Complexes Over General Cell Complexes
CW complexes offer superior flexibility in topological constructions compared to general cell complexes by allowing cells to be attached via arbitrary continuous maps instead of strict attaching conditions. This flexibility facilitates more effective homotopy-theoretic techniques, enabling better manipulation and simplification of spaces for algebraic topology purposes. The structure of CW complexes also ensures nicer closure-finiteness and weak topology properties that improve computational tractability in homology and cohomology theories.
Applications in Algebraic Topology
Cell complexes provide a foundational framework for constructing topological spaces by gluing cells of various dimensions, enabling the calculation of homology groups through cellular homology. CW complexes refine cell complexes with closure-finite and weak topology conditions, enhancing computational tractability and enabling the application of spectral sequences and cohomology theories. The structured nature of CW complexes is essential for calculating homotopy groups, classifying fiber bundles, and facilitating the study of characteristic classes in algebraic topology.
Summary: Choosing Between Cell and CW Complexes
Cell complexes provide a foundational framework for topological spaces constructed from cells, enabling straightforward manipulation and visualization, while CW complexes offer enhanced flexibility through closure-finite and weak topology conditions, facilitating advanced homotopy and homology analysis. CW complexes are preferred in algebraic topology due to their inductive construction and well-behaved attaching maps, supporting cellular homology computations. Choosing between cell and CW complexes depends on the balance between simplicity for geometric intuition and the need for rigorous algebraic topology tools.
Cell complex Infographic
 libterm.com
libterm.com