Natural transformation is a process used by bacteria to uptake and integrate free genetic material from their environment into their own genome, enhancing genetic diversity and adaptability. This mechanism plays a critical role in horizontal gene transfer, contributing to the spread of beneficial traits such as antibiotic resistance. Discover how natural transformation influences microbial evolution and its implications for biotechnology by reading the rest of the article.
Table of Comparison
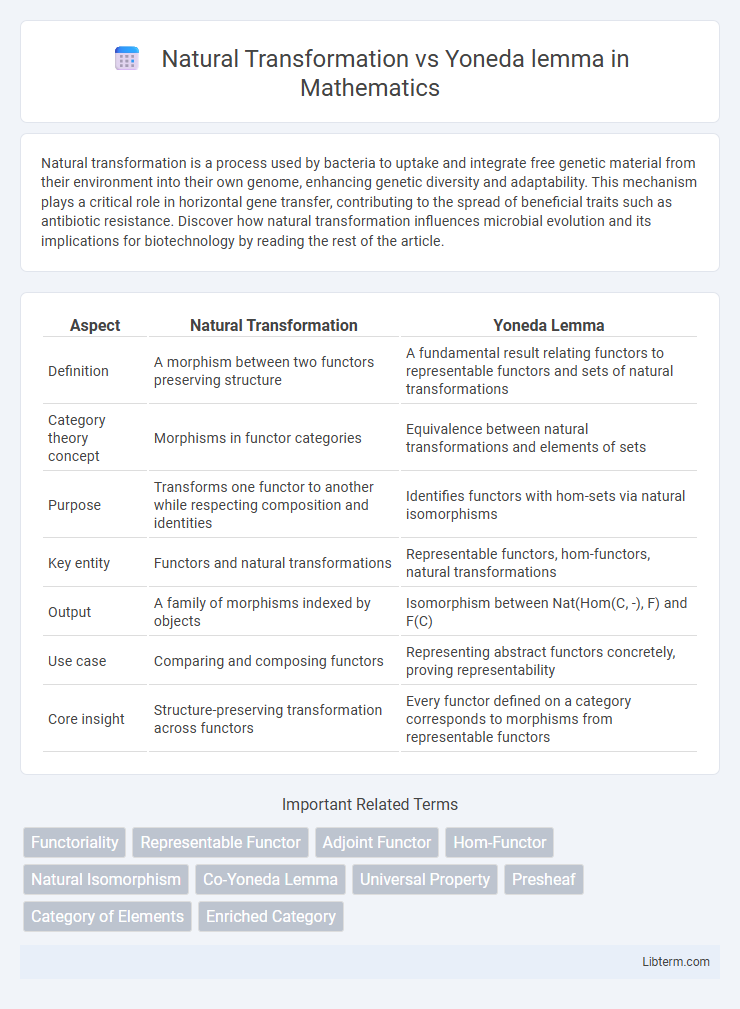
| Aspect | Natural Transformation | Yoneda Lemma |
|---|---|---|
| Definition | A morphism between two functors preserving structure | A fundamental result relating functors to representable functors and sets of natural transformations |
| Category theory concept | Morphisms in functor categories | Equivalence between natural transformations and elements of sets |
| Purpose | Transforms one functor to another while respecting composition and identities | Identifies functors with hom-sets via natural isomorphisms |
| Key entity | Functors and natural transformations | Representable functors, hom-functors, natural transformations |
| Output | A family of morphisms indexed by objects | Isomorphism between Nat(Hom(C, -), F) and F(C) |
| Use case | Comparing and composing functors | Representing abstract functors concretely, proving representability |
| Core insight | Structure-preserving transformation across functors | Every functor defined on a category corresponds to morphisms from representable functors |
Introduction to Natural Transformation and Yoneda Lemma
Natural transformations provide a way to compare functors by mapping one functor to another while preserving the structure between categories. The Yoneda Lemma establishes a fundamental relationship between objects in a category and sets of natural transformations from representable functors, revealing that every presheaf is determined by its action on representable functors. This lemma underpins much of category theory by demonstrating that an object can be fully understood through its relationships via natural transformations.
Foundational Concepts in Category Theory
Natural transformations serve as morphisms between functors, preserving the categorical structure and enabling comparisons within functor categories. The Yoneda lemma provides a foundational insight by establishing an isomorphism between natural transformations from a representable functor to any other functor and elements of the target functor's value at a specific object. Together, these concepts underpin the understanding of representability and functorial behavior in category theory.
Understanding Functors: The Building Blocks
Natural transformations serve as morphisms between functors, enabling a structured comparison of their actions on categories. The Yoneda lemma characterizes functors by establishing a bijection between natural transformations from a hom-functor to any functor and the elements of that functor evaluated at a specific object. Understanding functors as foundational elements clarifies how natural transformations reveal the relationships between different functors, while the Yoneda lemma formalizes these connections in category theory.
Defining Natural Transformations
Natural transformations are mappings between functors that preserve the categorical structure, associating each object in one category with a morphism in another while maintaining naturality conditions. The Yoneda lemma leverages natural transformations by characterizing functors from a category to Set in terms of morphisms from representable functors, revealing a deep connection between objects and natural transformations. Defining natural transformations requires specifying a component morphism for every object in the domain category subject to the commutativity of naturality squares, ensuring compatibility across all morphisms.
The Yoneda Lemma: Statement and Intuition
The Yoneda Lemma states that for any functor \( F: \mathcal{C} \to \mathbf{Set} \) and any object \( A \) in \( \mathcal{C} \), there is a natural isomorphism between the set of natural transformations from the hom-functor \( \text{Hom}(A, -) \) to \( F \) and the set \( F(A) \). This lemma provides an intuitive way to understand objects in a category by examining how they relate to other objects through morphisms, effectively embedding any object into the functor category. By representing objects as natural transformations, the Yoneda Lemma bridges abstract category theory with concrete set-valued functors, highlighting its foundational role in understanding natural transformations.
Key Differences Between Natural Transformations and Yoneda Lemma
Natural transformations provide a way to compare functors by assigning morphisms between their images that respect the categorical structure, serving as morphism-level mappings in functor categories. The Yoneda lemma establishes a fundamental isomorphism between natural transformations from a hom-functor to any functor and the elements of that functor, enabling concrete representation of abstract functors via sets of natural transformations. Key differences lie in natural transformations being explicit structure-preserving maps between functors, whereas the Yoneda lemma is an isomorphism that characterizes functors in terms of hom-sets and natural transformations.
Interplay: How Natural Transformation Relates to Yoneda Lemma
Natural transformations serve as morphisms between functors, encapsulating a systematic way of transforming one functor into another while preserving categorical structure. The Yoneda Lemma leverages natural transformations to establish a bijective correspondence between natural transformations from a representable functor to any functor and the elements of that functor at the representing object. This interplay showcases how natural transformations concretely realize the abstract equivalences posited by the Yoneda Lemma, grounding functorial relationships in element-level correspondences.
Applications in Mathematics and Computer Science
Natural transformations provide a framework for relating functors, enabling the comparison of different mathematical structures and facilitating the construction of universal properties in category theory. The Yoneda lemma offers a powerful tool for embedding categories into functor categories, simplifying the study of objects through representable functors and enabling canonical isomorphisms critical in algebraic geometry and homological algebra. In computer science, particularly in programming language theory and type systems, natural transformations model polymorphic functions, while the Yoneda lemma underpins optimizations and reasoning about data types and higher-order abstractions.
Visualizing Concepts: Diagrams and Examples
Natural transformations can be visualized as a family of morphisms connecting functors, represented by commutative diagrams illustrating how each component respects the structure of category transformations. The Yoneda lemma is often depicted through diagrams showing the natural isomorphism between hom-functors and sets of natural transformations, emphasizing representability and universal properties. Visual examples include commutative squares for naturality and representable functors mapped onto categories, providing intuitive insight into abstract categorical relationships.
Conclusion: Insights and Further Reading
Natural transformations provide a framework for comparing functors by mapping between categories, revealing deep structural relationships in category theory. The Yoneda Lemma characterizes how an object can be fully understood through its morphisms, offering a powerful tool for embedding and representing categories. Exploring these concepts together enriches understanding of categorical constructs, with further reading recommended in works by Mac Lane and Awodey for advanced applications and theoretical insights.
Natural Transformation Infographic
 libterm.com
libterm.com