A Verschiebung map is a fundamental concept in algebraic topology and homological algebra, representing a shift operator that moves elements within graded modules or complexes. This map plays a key role in understanding the structure of spectral sequences and cohomology theories. Explore the article to discover how Verschiebung maps influence advanced mathematical frameworks and their applications.
Table of Comparison
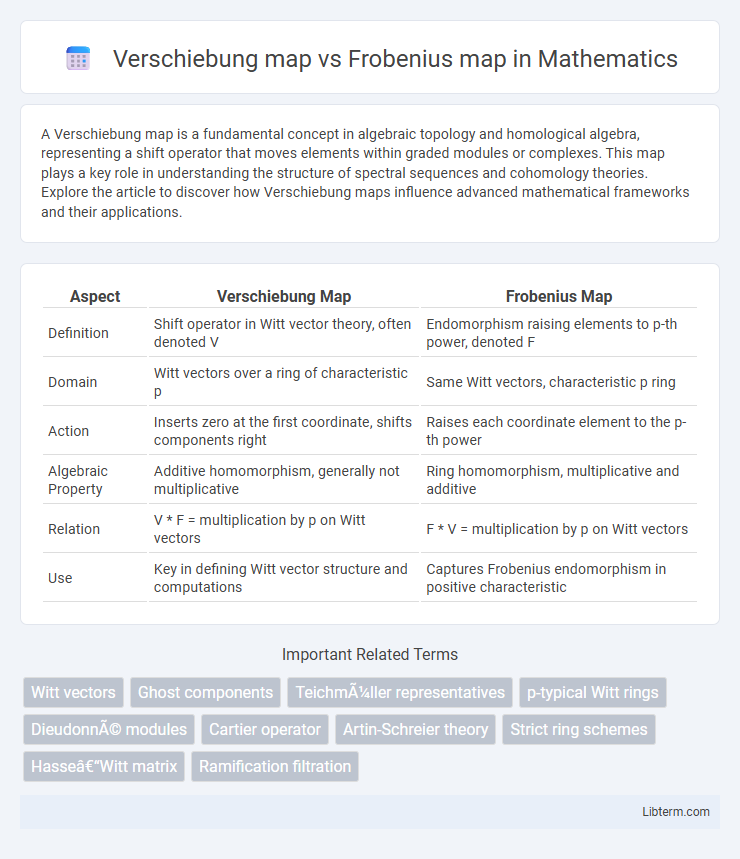
| Aspect | Verschiebung Map | Frobenius Map |
|---|---|---|
| Definition | Shift operator in Witt vector theory, often denoted V | Endomorphism raising elements to p-th power, denoted F |
| Domain | Witt vectors over a ring of characteristic p | Same Witt vectors, characteristic p ring |
| Action | Inserts zero at the first coordinate, shifts components right | Raises each coordinate element to the p-th power |
| Algebraic Property | Additive homomorphism, generally not multiplicative | Ring homomorphism, multiplicative and additive |
| Relation | V * F = multiplication by p on Witt vectors | F * V = multiplication by p on Witt vectors |
| Use | Key in defining Witt vector structure and computations | Captures Frobenius endomorphism in positive characteristic |
Introduction to Verschiebung and Frobenius Maps
The Verschiebung map is a key operator in the theory of Witt vectors and formal group laws, acting as a "shift" map that raises elements to a higher power of the prime p, often viewed as the adjoint of the Frobenius map. The Frobenius map, fundamental in algebraic geometry and number theory, raises each element to its p-th power, serving as a critical endomorphism in characteristic p rings and fields. Both maps interact intricately in the structure of p-typical Witt vectors, where Frobenius is a ring homomorphism and Verschiebung is a p-linear map satisfying the relation Frobenius * Verschiebung = multiplication by p.
Historical Context and Mathematical Significance
The Verschiebung map and Frobenius map are fundamental morphisms in the theory of algebraic groups and arithmetic geometry, particularly in positive characteristic p. Introduced in the early 20th century, the Frobenius map raises coordinates to the p-th power and plays a crucial role in the study of fields and schemes over finite fields, while the Verschiebung map acts as a sort of "adjoint" operator reversing the Frobenius on Witt vectors and finite group schemes. These maps underpin the structure of p-divisible groups and Dieudonne modules, linking number theory, algebraic geometry, and representation theory through their impact on the classification of abelian varieties and Galois representations.
Definitions: Verschiebung Map Explained
The Verschiebung map is an additive operator acting on Witt vectors, defined as a shift that inserts a zero in the first coordinate and shifts the remaining components one position to the right. Unlike the Frobenius map, which raises each Witt vector component to the p-th power and compresses coordinates, the Verschiebung map acts as a left inverse to Frobenius in characteristic p. This operator plays a critical role in the theory of Dieudonne modules and is essential for understanding the structure of formal group laws and p-divisible groups.
Definitions: Frobenius Map Explained
The Frobenius map, fundamental in arithmetic geometry, raises each element of a ring of characteristic p to its p-th power, serving as a ring homomorphism that preserves the algebraic structure. The Verschiebung map, often defined in the context of Witt vectors, acts as a left inverse to the Frobenius map and shifts components, playing a crucial role in the theory of p-typical formal group laws. Understanding the Frobenius map involves recognizing its function as an endomorphism that encapsulates the action of raising elements to powers of the characteristic prime, while Verschiebung complements this by enabling the manipulation of Witt vector components in advanced number theory.
Algebraic Structures Involving Both Maps
The Verschiebung map and Frobenius map operate as fundamental endomorphisms within the structure of Witt vectors and Dieudonne modules, where the Frobenius acts by raising coordinates to the p-th power while Verschiebung serves as its adjoint operator. These maps satisfy key relations such as the commutation \(F \circ V = V \circ F = p\), encoding deep arithmetic properties in the category of commutative group schemes over fields of characteristic \(p\). Their interplay governs the structure of p-divisible groups and crystalline cohomology, linking algebraic geometry with characteristic p phenomena in arithmetic geometry.
Key Differences: Verschiebung vs Frobenius
The Verschiebung map acts as a "shift" operator on the Witt vectors, raising components while inserting zeros, whereas the Frobenius map raises each component to the p-th power, acting as an endomorphism. Verschiebung is additive but not multiplicative, contrasting with Frobenius, which is multiplicative but generally not additive. Key algebraic identities include the relations FV = VF = p, highlighting their complementary roles in the structure of Witt rings and crystalline cohomology.
Interactions in Witt Vectors
The Verschiebung map and Frobenius map are fundamental operators acting on Witt vectors, where the Frobenius map raises each component to the p-th power while the Verschiebung map shifts components, inserting zero at the beginning. These maps interact such that their composition satisfies FrobeniusVerschiebung = multiplication by p, establishing a crucial relationship for the structure of the ring of Witt vectors. This interaction plays a key role in describing the arithmetic and cohomological properties of rings in characteristic p through the Witt vector formalism.
Applications in Number Theory and Algebraic Geometry
The Verschiebung and Frobenius maps play crucial roles in the study of abelian varieties and p-divisible groups, with applications in the classification of isogeny classes and the structure of Dieudonne modules. The Frobenius map acts as a fundamental endomorphism in characteristic p fields, influencing the behavior of etale cohomology and the analysis of zeta functions of algebraic varieties. Verschiebung serves as the adjoint of Frobenius, facilitating the exploration of deformation theory and crystalline cohomology, which are essential tools in modern algebraic geometry and arithmetic geometry.
Typical Examples and Computations
The Verschiebung map, typically denoted as V, is essential in the theory of finite commutative group schemes over fields of positive characteristic p, often serving as a left adjoint to the Frobenius map F. In standard examples such as the group scheme of p-typical Witt vectors \( W_n \), the Frobenius map raises each coordinate to the p-th power, while the Verschiebung map shifts coordinates rightward, introducing zeros on the left. Computations in Dieudonne theory reveal that these maps satisfy the relation \(FV = VF = p\), which is crucial in understanding the structure of p-divisible groups and their Dieudonne modules.
Conclusion: Importance in Modern Mathematics
The Verschiebung map and Frobenius map are fundamental in arithmetic geometry and the theory of modular forms, playing crucial roles in the structure of p-divisible groups and crystalline cohomology. Their interplay provides deep insights into the behavior of algebraic varieties over fields of positive characteristic, facilitating advances in the study of deformation theory and Galois representations. Understanding these maps underpins significant progress in modern number theory, including the proof of key conjectures like the Fontaine-Mazur conjecture and the development of p-adic Hodge theory.
Verschiebung map Infographic
 libterm.com
libterm.com