A covariate is an independent variable that can influence the outcome of a study or experiment, potentially affecting the relationship between the primary variables under investigation. Properly accounting for covariates is crucial to ensure accurate and unbiased results in statistical analyses. Explore the rest of the article to understand how covariates impact data interpretation and study design.
Table of Comparison
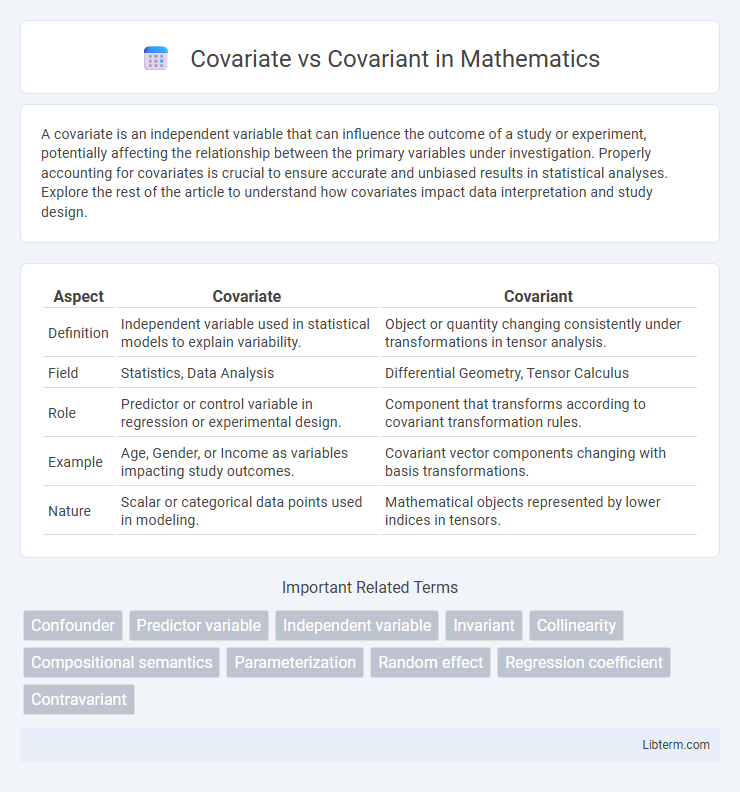
| Aspect | Covariate | Covariant |
|---|---|---|
| Definition | Independent variable used in statistical models to explain variability. | Object or quantity changing consistently under transformations in tensor analysis. |
| Field | Statistics, Data Analysis | Differential Geometry, Tensor Calculus |
| Role | Predictor or control variable in regression or experimental design. | Component that transforms according to covariant transformation rules. |
| Example | Age, Gender, or Income as variables impacting study outcomes. | Covariant vector components changing with basis transformations. |
| Nature | Scalar or categorical data points used in modeling. | Mathematical objects represented by lower indices in tensors. |
Understanding Covariate and Covariant: Definitions
Covariate refers to an independent variable or factor that may influence the outcome in statistical analyses, often used to control for potential confounding effects in regression models. Covariant describes a mathematical object or property that transforms in a specific way under a change of basis, particularly in tensor calculus and physics, preserving its form relative to coordinate transformations. Understanding these definitions highlights that covariates pertain to statistical modeling, while covariant relates to invariant transformation properties in mathematics and physics.
Key Differences Between Covariate and Covariant
Covariate refers to an independent variable in statistical analysis that can influence the outcome of a study, while covariant relates to the property of objects or functions changing in a specific way under transformations in mathematics and physics. Covariates are used to control confounding effects in regression models, whereas covariants describe how quantities transform under coordinate changes, especially in tensor calculus. The key difference lies in their domains and applications: covariates pertain to data analysis, and covariants are fundamental in differential geometry and theoretical physics.
Real-World Examples of Covariates and Covariants
Covariates frequently appear in statistical models such as linear regression where variables like age, income, or education level influence the outcome without being manipulated, helping to control for confounding factors in studies on health or economics. Covariants arise in programming and physics, exemplified by covariant type parameters in object-oriented languages like Scala that preserve subtype relationships, or tensors in general relativity whose components transform covariantly under coordinate changes. Real-world data analysis distinguishes covariates as measured predictors while software development leverages covariant types to ensure type safety in polymorphic functions.
Covariate in Statistics: Role and Importance
Covariates in statistics represent variables that potentially influence the outcome of a study and are included in models to control for confounding effects, thereby improving the accuracy of estimated relationships between independent and dependent variables. Their importance lies in enhancing model precision, reducing bias, and enabling clearer interpretations of causal effects in experimental and observational research. Proper identification and incorporation of covariates lead to more reliable statistical inferences and optimized predictive performance.
Covariant in Mathematics: Concept and Applications
Covariant in mathematics refers to objects or quantities that transform in a specific way under a change of basis, preserving the form of equations in tensor calculus and differential geometry. Covariant vectors, or covectors, belong to the dual space and adjust according to the inverse transpose of the transformation applied to the base vectors, ensuring consistency in coordinate transformations. Applications of covariant concepts are crucial in physics, particularly in general relativity, where tensors describe physical phenomena irrespective of the observer's frame of reference.
Common Misconceptions: Covariate vs Covariant
Covariate and covariant are often confused due to their similar spellings, but they have distinct meanings in statistics and mathematics. A covariate refers to an independent variable in regression analysis that potentially influences the dependent variable, while covariant describes variables or quantities that transform in a compatible way under coordinate changes in tensor calculus or physics. Misunderstanding these terms can lead to errors in model specification or mathematical interpretation, especially in interdisciplinary research contexts.
How to Identify a Covariate in Data Analysis
A covariate in data analysis is an independent variable that potentially influences the dependent variable and is measured alongside the primary variables of interest. To identify a covariate, examine variables that are not the main focus but affect the outcome, such as age, gender, or baseline measurements, and include these in regression models to control for confounding effects. Statistical tests and correlation analyses help determine the relationship strength between potential covariates and the dependent variable, ensuring accurate interpretation of the model results.
Exploring Covariant Transformations in Geometry
Covariant transformations refer to the way geometric objects such as vectors and tensors change under coordinate transformations, preserving their intrinsic relationships. In geometry, covariant components transform according to the basis change, ensuring that physical laws remain consistent regardless of the coordinate system. Understanding covariant transformations is essential for studying manifolds, tensor fields, and the differential geometry underlying general relativity and advanced mathematical physics.
Practical Applications of Covariate and Covariant
Covariates play a crucial role in statistical modeling and experimental designs by serving as control variables that help isolate the effect of the primary independent variables, thereby enhancing the accuracy of causal inferences and predictions. Covariants are fundamental in computer science, especially in type theory and programming languages, where they enable subtype relationships to be preserved during method overriding and generic type assignments, facilitating safer and more flexible code reuse. Practical applications of covariates include epidemiological studies adjusting for confounding factors, while covariant concepts are instrumental in designing type-safe APIs and supporting polymorphism in object-oriented programming.
Summary: Covariate vs Covariant at a Glance
Covariate refers to an external variable in statistical models that may influence the outcome, used to control for confounding effects in regression analysis. Covariant describes a property of mathematical objects, particularly tensors or vectors, that transform consistently under coordinate changes in geometry and physics. Understanding covariate in statistics versus covariant in mathematics clarifies their distinct roles in data analysis and theoretical frameworks.
Covariate Infographic
 libterm.com
libterm.com