Fusion categories are algebraic structures that play a crucial role in fields such as quantum physics, topology, and category theory, characterized by objects that can be combined via a tensor product with associativity and duals. Their study involves understanding fusion rules, modular data, and applications in topological quantum computation. Explore this article to deepen Your knowledge of fusion categories and their significant mathematical and physical implications.
Table of Comparison
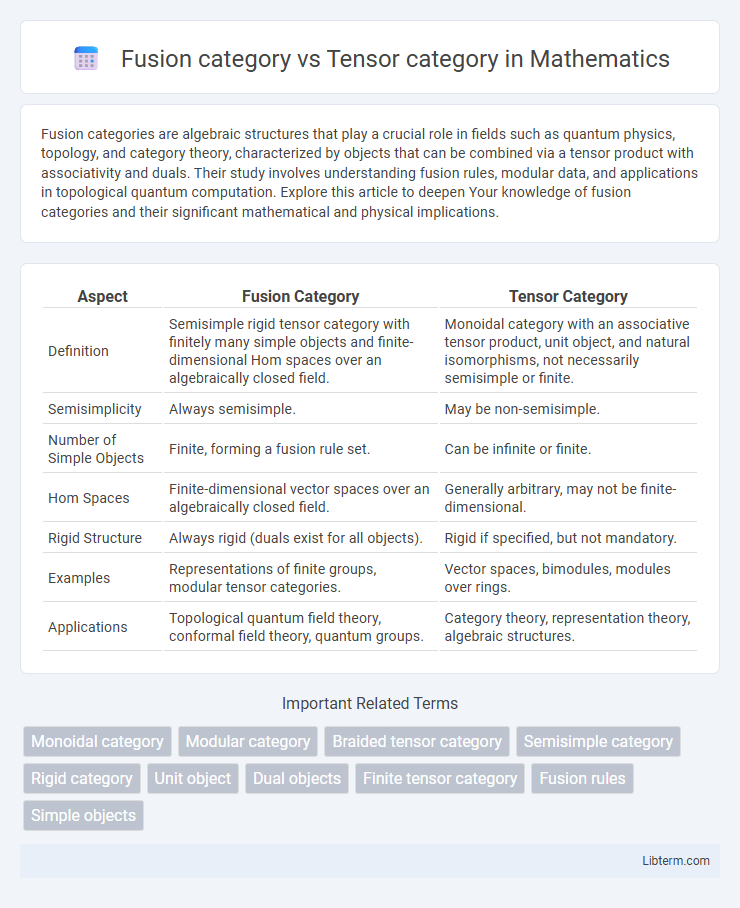
| Aspect | Fusion Category | Tensor Category |
|---|---|---|
| Definition | Semisimple rigid tensor category with finitely many simple objects and finite-dimensional Hom spaces over an algebraically closed field. | Monoidal category with an associative tensor product, unit object, and natural isomorphisms, not necessarily semisimple or finite. |
| Semisimplicity | Always semisimple. | May be non-semisimple. |
| Number of Simple Objects | Finite, forming a fusion rule set. | Can be infinite or finite. |
| Hom Spaces | Finite-dimensional vector spaces over an algebraically closed field. | Generally arbitrary, may not be finite-dimensional. |
| Rigid Structure | Always rigid (duals exist for all objects). | Rigid if specified, but not mandatory. |
| Examples | Representations of finite groups, modular tensor categories. | Vector spaces, bimodules, modules over rings. |
| Applications | Topological quantum field theory, conformal field theory, quantum groups. | Category theory, representation theory, algebraic structures. |
Introduction to Fusion and Tensor Categories
Fusion categories are pivotal algebraic structures in representation theory and quantum algebra, characterized by semisimplicity, finiteness, and rigidity, with simple objects closed under tensor product operations. Tensor categories generalize fusion categories, allowing infinite objects or non-semisimple structures, and are equipped with a monoidal tensor product and associativity constraints that facilitate the study of module categories and higher categorical frameworks. Understanding fusion categories as semisimple, finite tensor categories with duals provides foundational insights into modular tensor categories and topological quantum field theories.
Defining Tensor Categories
Tensor categories are rigid monoidal categories equipped with duals, associativity constraints, and unit objects, serving as a foundational framework in representation theory and quantum algebra. Fusion categories are a special class of semisimple tensor categories with finitely many simple objects, finite-dimensional Hom spaces, and simple tensor units, often arising in topological quantum field theory and conformal field theory. Defining tensor categories involves specifying the monoidal structure, associators, unitors, and duals, which collectively determine the category's coherence and duality properties.
Key Concepts in Fusion Categories
Fusion categories are semisimple rigid tensor categories with finitely many simple objects, finite-dimensional Hom spaces, and simple unit object, playing a crucial role in representation theory and topological quantum field theory. Key concepts include the fusion rules describing how simple objects tensor together, the pivotal structure enabling duality, and the categorical dimensions giving important invariants. Unlike general tensor categories, fusion categories have strict semisimplicity and finiteness conditions that ensure tractable and physically meaningful fusion algebra structures.
Comparison: Fusion vs Tensor Categories
Fusion categories are semisimple rigid tensor categories with finitely many simple objects and finite-dimensional Hom spaces, while tensor categories may lack semisimplicity and finiteness conditions. Fusion categories possess a pivotal structure and duals for every object, enabling applications in topological quantum field theory and conformal field theory. Tensor categories provide a broader framework encompassing fusion categories, allowing for more general objects and morphisms without the strict constraints of fusion categories.
Examples of Fusion Categories
Fusion categories are semisimple rigid monoidal categories with finitely many simple objects and finite-dimensional Hom spaces, often arising in representation theory, quantum groups, and topological quantum field theory. Examples of fusion categories include the representation category of a finite group (Rep(G)), the category of representations of a quantum group at a root of unity, and the Tambara-Yamagami categories characterized by a finite abelian group with a non-degenerate symmetric bicharacter. Tensor categories broadly encompass fusion categories but may lack semisimplicity or finiteness conditions, making fusion categories a specialized and highly structured subclass crucial for applications in low-dimensional topology and conformal field theory.
Notable Tensor Categories in Mathematics
Fusion categories are semisimple, rigid tensor categories with finitely many simple objects and are pivotal in areas like topological quantum field theory and quantum groups. Notable tensor categories include braided tensor categories arising in conformal field theory and modular tensor categories that provide invariants for 3-manifolds. Tensor categories also encompass representation categories of quantum groups, illustrating deep connections between algebra, topology, and category theory.
Applications in Physics and Mathematics
Fusion categories provide a powerful algebraic framework for modeling topological phases of matter and anyonic excitations in condensed matter physics, enabling the classification of low-dimensional quantum systems. Tensor categories, more broadly, encompass fusion categories and are crucial in the study of quantum groups, conformal field theory, and representation theory, facilitating the understanding of symmetries and dualities in mathematical physics. Their algebraic structures support the formulation of invariants in 3-manifold topology and play a significant role in categorifying quantum invariants and topological quantum computing.
Structural Properties and Differences
Fusion categories are semisimple rigid tensor categories with finitely many simple objects, simple unit, and duals that ensure pivotal structure, emphasizing finiteness and modularity in their structure. Tensor categories are broader, encompassing categories with an associative tensor product and unit object but not necessarily semisimple or finite, allowing more general algebraic and categorical phenomena. The key structural difference is that fusion categories require semisimplicity and finiteness of simple objects, while tensor categories impose fewer constraints, enabling applications in diverse algebraic and quantum contexts.
Morphisms and Functorial Aspects
Fusion categories are semisimple, rigid tensor categories with finitely many simple objects and finite-dimensional Hom spaces, emphasizing duality and pivotal structures in their morphisms. Tensor categories generalize fusion categories without requiring semisimplicity or finiteness, allowing a broader class of morphisms including non-invertible and infinite-dimensional cases. Functorial aspects in fusion categories involve monoidal functors preserving duals and pivotal structures, while in tensor categories, functors may relax these constraints, impacting coherence, rigidity, and equivalence classifications.
Future Directions in Category Theory
Future directions in category theory emphasize deepening the understanding of fusion categories through advanced tensor categorical frameworks that unify algebraic and topological quantum field theories. Research aims to develop comprehensive classification methods leveraging higher category theory and modular tensor categories to tackle complex phenomena in condensed matter physics and quantum computation. Expanding applications in homotopy theory and braided fusion category structures will drive innovations in mathematical physics and quantum information science.
Fusion category Infographic
 libterm.com
libterm.com