Kan extensions provide a powerful framework in category theory for generalizing and unifying concepts like limits, colimits, and adjunctions within mathematical structures. Understanding Kan extensions allows you to analyze how functors can be optimally extended or restricted between categories while preserving essential properties. Dive into the rest of this article to explore the fundamental principles, examples, and applications of Kan extensions in depth.
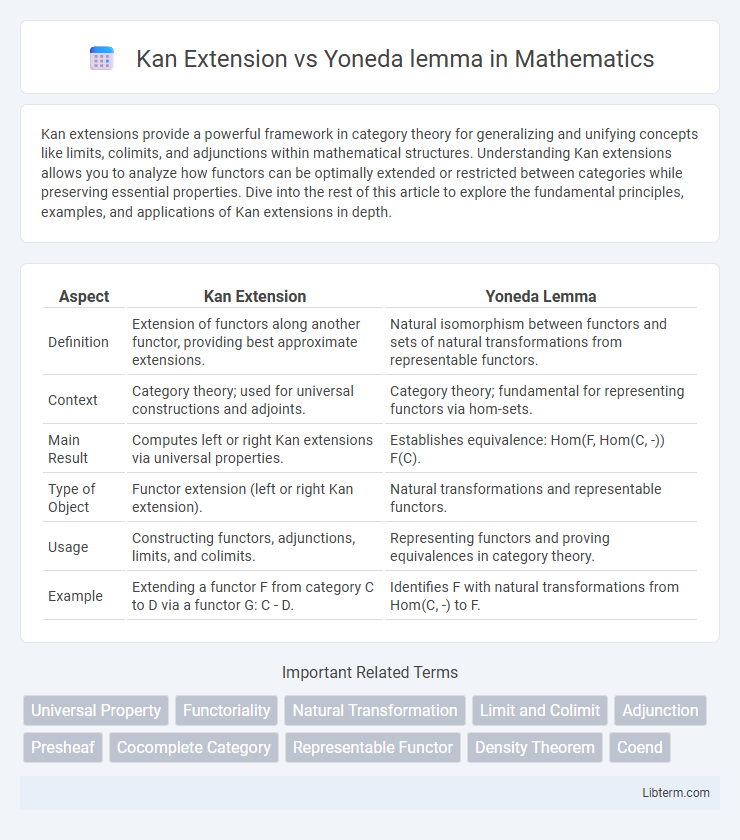
Table of Comparison
| Aspect | Kan Extension | Yoneda Lemma |
|---|---|---|
| Definition | Extension of functors along another functor, providing best approximate extensions. | Natural isomorphism between functors and sets of natural transformations from representable functors. |
| Context | Category theory; used for universal constructions and adjoints. | Category theory; fundamental for representing functors via hom-sets. |
| Main Result | Computes left or right Kan extensions via universal properties. | Establishes equivalence: Hom(F, Hom(C, -)) F(C). |
| Type of Object | Functor extension (left or right Kan extension). | Natural transformations and representable functors. |
| Usage | Constructing functors, adjunctions, limits, and colimits. | Representing functors and proving equivalences in category theory. |
| Example | Extending a functor F from category C to D via a functor G: C - D. | Identifies F with natural transformations from Hom(C, -) to F. |
Introduction to Kan Extension and Yoneda Lemma
Kan Extensions generalize the concept of extending functors along other functors, providing a universal way to approximate or extend mappings between categories. The Yoneda Lemma establishes a fundamental correspondence between objects in a category and natural transformations from representable functors, revealing deep insights about objects via their hom-sets. Both concepts are central in category theory, with Kan Extensions enabling the construction of new functors and the Yoneda Lemma offering a powerful tool for studying categorical structures through representability.
Fundamental Concepts in Category Theory
Kan extensions generalize the notion of extending functors along other functors, providing a universal approximation framework crucial in defining limits and colimits in category theory. The Yoneda lemma establishes a natural isomorphism between hom-sets and sets of natural transformations, serving as a foundational tool to embed categories into functor categories. Both concepts are fundamental: Kan extensions focus on universality and functorial extension, while the Yoneda lemma underpins representability and fully faithful embeddings.
Defining the Kan Extension
Kan extension generalizes the process of extending functors along other functors, forming a universal construction in category theory that captures how information is transferred between categories. It is defined by a pair of adjoint functors, typically a left Kan extension as a left adjoint that extends a functor while preserving colimits, and a right Kan extension as a right adjoint preserving limits. The Yoneda lemma provides foundational insight by embedding categories into presheaf categories, allowing Kan extensions to be explicitly computed in terms of natural transformations from representable functors.
Understanding the Yoneda Lemma
The Yoneda Lemma reveals a fundamental isomorphism between a functor and the natural transformations from representable functors, providing a powerful tool to analyze and reconstruct objects in category theory. Understanding the Yoneda Lemma enables the identification of any presheaf as a colimit of representable functors, thus simplifying complex categorical structures. This insight is crucial for leveraging Kan extensions, as Kan extensions generalize the concept of limits and colimits, often computed via representable functors described by the Yoneda Lemma.
Mathematical Formulations: Kan Extension vs Yoneda Lemma
Kan extensions generalize the notion of extending a functor along another functor, characterized by universal properties involving limits or colimits, specifically defined as the right or left Kan extension using natural transformations. The Yoneda lemma provides a natural isomorphism between the set of natural transformations from the Hom-functor to any functor, effectively embedding any category into a presheaf category and expressing objects via representable functors. While Kan extensions focus on functorial extension and universal constructions in diagram categories, the Yoneda lemma offers a foundational representation theorem that enables the characterization of objects and morphisms through hom-sets and natural transformations.
Key Differences Between Kan Extension and Yoneda Lemma
Kan Extension generalizes the extension of functors along other functors, providing a universal solution to lifting or restricting functors between categories, while the Yoneda Lemma establishes a concrete isomorphism between natural transformations from hom-functors to any functor and the set evaluated at a specific object. Kan Extension is a broader categorical construction often involving colimits or limits to define extensions, whereas the Yoneda Lemma specifically characterizes representable functors and natural transformations, serving as a foundational result in category theory. The key difference lies in Kan Extension's role in functorial extension and universality versus the Yoneda Lemma's explicit correspondence highlighting representability and embedding of categories.
Use Cases and Applications in Mathematics
Kan extensions provide a powerful framework for defining and studying universal properties in category theory, enabling the construction of new functors from existing ones with applications in homological algebra and algebraic topology. The Yoneda lemma offers a foundational tool for embedding categories into functor categories, facilitating the representation of objects by their hom-sets and optimizing the analysis of natural transformations in algebraic geometry and representation theory. Together, these concepts serve as essential methods for generalizing and solving problems related to limits, colimits, and adjoint functors across various branches of mathematics.
Interconnections and Relationships
Kan extensions and the Yoneda lemma share foundational roles in category theory, with Kan extensions generalizing the process of extending functors and the Yoneda lemma providing a precise characterization of natural transformations via hom-functors. The Yoneda lemma serves as a critical tool to express how objects relate to representable functors, which in turn facilitates understanding Kan extensions as universal constructions defined by natural transformations between functors. Their interconnection lies in the way the Yoneda lemma underpins the formulation of Kan extensions, enabling explicit computations of left and right Kan extensions through representable functors and natural isomorphisms.
Comparative Advantages and Limitations
Kan Extensions provide a universal way to extend functors along other functors, allowing for the construction of new functors while preserving existing structures, which is essential in category theory for defining limits and colimits. The Yoneda Lemma offers a powerful characterization of functors by representing them as sets of natural transformations, enabling a deep understanding of object representability and embedding categories into presheaf categories. While Kan Extensions excel in constructing and comparing functors in complex diagrams, they can be abstract and computationally challenging, whereas the Yoneda Lemma simplifies representability problems but is primarily a tool for theoretical insight rather than explicit construction.
Conclusion: Choosing Between Kan Extension and Yoneda Lemma
Kan Extension provides a powerful tool for extending functors along other functors, often used for constructing universal objects and understanding colimits in category theory. The Yoneda Lemma offers a fundamental characterization of presheaves by embedding categories into functor categories, enabling concrete representations of abstract concepts. Choosing between Kan Extension and Yoneda Lemma depends on whether the goal is to extend functorial behavior (Kan Extension) or to represent objects via natural transformations and hom-functors (Yoneda Lemma).
Kan Extension Infographic
 libterm.com
libterm.com