Fourier series decompose complex periodic signals into sums of sine and cosine components, enabling the analysis of frequency content in functions. This mathematical tool is essential in fields such as signal processing, acoustics, and electrical engineering for understanding waveforms. Discover how Fourier series can transform your approach to analyzing periodic phenomena by reading the rest of this article.
Table of Comparison
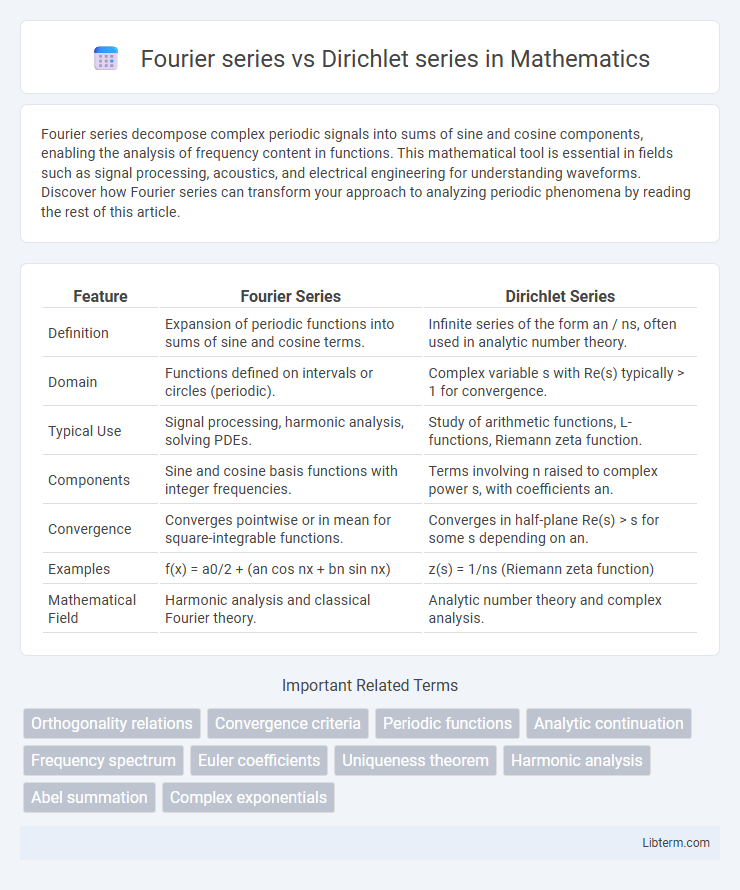
| Feature | Fourier Series | Dirichlet Series |
|---|---|---|
| Definition | Expansion of periodic functions into sums of sine and cosine terms. | Infinite series of the form an / ns, often used in analytic number theory. |
| Domain | Functions defined on intervals or circles (periodic). | Complex variable s with Re(s) typically > 1 for convergence. |
| Typical Use | Signal processing, harmonic analysis, solving PDEs. | Study of arithmetic functions, L-functions, Riemann zeta function. |
| Components | Sine and cosine basis functions with integer frequencies. | Terms involving n raised to complex power s, with coefficients an. |
| Convergence | Converges pointwise or in mean for square-integrable functions. | Converges in half-plane Re(s) > s for some s depending on an. |
| Examples | f(x) = a0/2 + (an cos nx + bn sin nx) | z(s) = 1/ns (Riemann zeta function) |
| Mathematical Field | Harmonic analysis and classical Fourier theory. | Analytic number theory and complex analysis. |
Introduction to Fourier Series and Dirichlet Series
Fourier series represent periodic functions as infinite sums of sines and cosines, enabling analysis of frequency components in signals and solving boundary value problems in engineering and physics. Dirichlet series, expressed as infinite sums involving terms of the form a_n/n^s, are fundamental in analytic number theory and are crucial for studying properties of arithmetic functions and the Riemann zeta function. Both series provide powerful tools for function representation, with Fourier series emphasizing harmonic decomposition and Dirichlet series focusing on multiplicative structures in integers.
Mathematical Foundations of Fourier Series
Fourier series decompose periodic functions into sums of sine and cosine terms, leveraging orthogonality properties of trigonometric functions defined on the interval \([-p, p]\). The mathematical foundation centers on representing square-integrable functions in the Hilbert space \(L^2([-p, p])\) through an orthonormal basis, enabling convergence in the mean-square sense. Unlike Dirichlet series, which use complex powers for analytic continuation and number-theoretic applications, Fourier series primarily analyze function behavior in the time or spatial domain using harmonic components.
Core Principles of Dirichlet Series
Dirichlet series fundamentally differ from Fourier series by expressing functions through sums of the form \(\sum_{n=1}^\infty \frac{a_n}{n^s}\), where \(s\) is a complex variable, enabling deep connections to number theory and analytic properties of arithmetic functions. The core principles of Dirichlet series involve convergence in half-planes of the complex plane and their analytic continuation, which are crucial in studying L-functions and the distribution of prime numbers. Unlike Fourier series that decompose periodic functions into trigonometric components, Dirichlet series harness multiplicative structures and complex analysis to encode arithmetic information.
Key Differences in Structure and Representation
Fourier series represent periodic functions using a sum of sines and cosines with coefficients corresponding to frequency components, providing a decomposition in the time domain. Dirichlet series, by contrast, involve sums of terms of the form a_n n^{-s}, where a_n are complex coefficients and s is a complex variable, primarily used in analytic number theory to study properties of arithmetic functions. The key structural difference lies in Fourier series depending on trigonometric bases related to real variables, while Dirichlet series rely on complex power functions indexed by positive integers, offering representations useful for understanding the distribution of prime numbers and zeta functions.
Convergence Criteria: Fourier vs. Dirichlet Series
Fourier series converge pointwise and uniformly under Dirichlet conditions, requiring piecewise continuity and bounded variation of the function on a finite interval. Dirichlet series converge in half-planes of the complex plane determined by their abscissa of convergence, governed by the behavior of partial sums and the real part of the complex variable. The convergence of Fourier series is tied to function smoothness, while Dirichlet series convergence relies on complex analysis and growth rates of coefficients.
Applications in Mathematics and Engineering
Fourier series decompose periodic functions into sums of sines and cosines, enabling efficient analysis of signals, vibrations, and heat transfer in engineering. Dirichlet series, characterized by sums of the form a_n/n^s, are fundamental in number theory for studying the distribution of prime numbers and in complex analysis for analytic continuation of L-functions. In applied mathematics, Fourier series excel in solving partial differential equations modeling wave propagation, while Dirichlet series serve critical roles in cryptographic algorithms and spectral theory.
Analytical Techniques for Both Series
Fourier series decompose periodic functions into sums of sine and cosine functions, employing orthogonality properties and Parseval's theorem for convergence analysis, while Dirichlet series represent arithmetic functions through infinite sums of terms involving n^(-s), crucial in analytic number theory and complex analysis. Analytical techniques for Fourier series emphasize uniform convergence, harmonic analysis, and pointwise convergence via Fejer's theorem, whereas Dirichlet series rely on complex analytic continuation, abscissa of convergence, and Perron's formula to study distribution of prime numbers. Both series utilize contour integration and residue calculus in complex planes, but Fourier series focus on real variable function decomposition, contrasting Dirichlet series' dependence on complex variable s and Euler products.
Comparative Examples and Illustrations
Fourier series decompose periodic functions into sums of sines and cosines, ideal for analyzing signals and heat distributions, while Dirichlet series represent functions as infinite sums of inverse powers weighted by coefficients, commonly used in number theory, such as in the Riemann zeta function. A Fourier series example expands f(x)=x on [-p,p] into a sine series capturing its odd symmetry, whereas the Dirichlet series z(s)=_{n=1}^ 1/n^s converges for complex s with real part greater than one, illustrating analytic properties in the complex plane. Fourier series typically handle periodicity and smoothness, while Dirichlet series probe arithmetic properties and prime distributions through analytic continuation and functional equations.
Advantages and Limitations of Each Series
Fourier series excel in representing periodic functions through sums of sines and cosines, offering strong convergence properties and broad applicability in signal processing and heat diffusion problems. Dirichlet series, commonly used in number theory and complex analysis, provide powerful tools for studying arithmetic functions through analytic continuation and prime number distributions but face limitations in representing general functions due to convergence restrictions. While Fourier series handle a wide range of functions with well-understood convergence on intervals, Dirichlet series are often constrained to half-planes and require complex variable techniques, limiting their direct application outside analytic number theory.
Conclusion: Choosing Between Fourier and Dirichlet Series
Fourier series excel in representing periodic functions through trigonometric expansions, making them ideal for signal processing and heat transfer problems. Dirichlet series, characterized by their form involving complex variables and number-theoretic coefficients, are primarily used in analytic number theory and the study of L-functions. Selecting between Fourier and Dirichlet series depends on the application context: Fourier series suit continuous, periodic phenomena, while Dirichlet series target discrete, arithmetic properties in complex analysis.
Fourier series Infographic
 libterm.com
libterm.com