Desingularization is a mathematical process that transforms singular spaces or objects into nonsingular, or smooth, forms to enable easier analysis and manipulation. It plays a crucial role in algebraic geometry and complex analysis, where singularities can complicate problem-solving and theoretical exploration. Discover how desingularization techniques can enhance your understanding by reading the rest of this article.
Table of Comparison
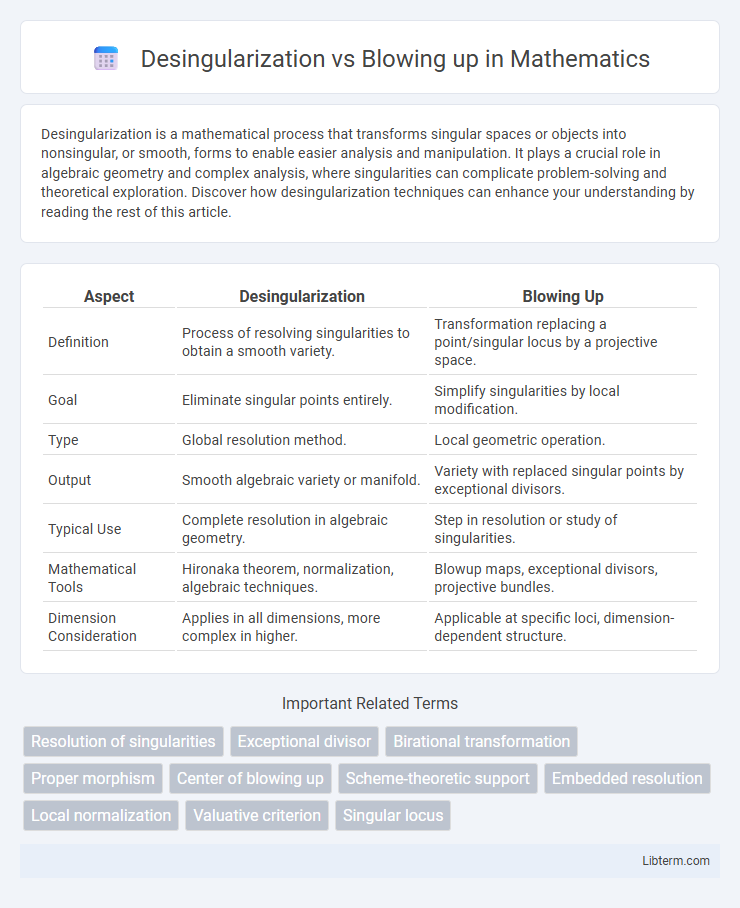
| Aspect | Desingularization | Blowing Up |
|---|---|---|
| Definition | Process of resolving singularities to obtain a smooth variety. | Transformation replacing a point/singular locus by a projective space. |
| Goal | Eliminate singular points entirely. | Simplify singularities by local modification. |
| Type | Global resolution method. | Local geometric operation. |
| Output | Smooth algebraic variety or manifold. | Variety with replaced singular points by exceptional divisors. |
| Typical Use | Complete resolution in algebraic geometry. | Step in resolution or study of singularities. |
| Mathematical Tools | Hironaka theorem, normalization, algebraic techniques. | Blowup maps, exceptional divisors, projective bundles. |
| Dimension Consideration | Applies in all dimensions, more complex in higher. | Applicable at specific loci, dimension-dependent structure. |
Introduction to Singularity Resolution
Singularity resolution involves techniques like desingularization and blowing up to transform singular algebraic varieties into smooth ones, facilitating their geometric and topological analysis. Desingularization systematically replaces singular points with simpler structures, often through a sequence of blowing up processes that isolate and resolve complex singularities. These methods are fundamental in algebraic geometry for studying the intrinsic properties of varieties and ensuring well-behaved morphisms.
Understanding Desingularization
Desingularization is a process in algebraic geometry aimed at resolving singularities by systematically replacing singular points with smoother structures, thereby creating a nonsingular variety or manifold. This technique is essential for understanding the local behavior of varieties and is often achieved through sequences of blowups, which are specific transformations that isolate and simplify singularities. Mastering desingularization enables mathematicians to analyze complex geometric objects with improved clarity and apply advanced theoretical tools more effectively.
The Concept of Blowing Up in Algebraic Geometry
Blowing up in algebraic geometry is a geometric transformation that replaces a subvariety with the space of its normal directions, effectively resolving singularities by spreading them out into a higher-dimensional space. This process enhances the structure of algebraic varieties by converting complicated singular points into simpler, more manageable components, often divisors called exceptional divisors. Blowing up plays a central role in desingularization, serving as a fundamental tool to systematically improve the geometry and smoothness of varieties.
Key Differences Between Desingularization and Blowing Up
Desingularization involves resolving singularities to produce a smooth variety, while blowing up replaces a point with an entire subvariety to study local structure without necessarily smoothing. Blowing up is a fundamental step within many desingularization processes but does not guarantee the removal of singularities alone. The key difference lies in desingularization aiming for a smooth variety, whereas blowing up locally transforms the space for detailed analysis.
Historical Development of Resolution Techniques
Desingularization and blowing up emerged as foundational techniques in algebraic geometry for resolving singularities, with blowing up introduced by Oscar Zariski in the mid-20th century as a geometric transformation to replace singular points with simpler structures. The historical development progressed with Heisuke Hironaka's groundbreaking 1964 proof of resolution of singularities in characteristic zero, which formalized desingularization as a systematic process involving sequences of blowups. These advancements laid the groundwork for modern resolution methods, influencing both complex algebraic varieties and arithmetic geometry.
Applications of Blowing Up in Geometry
Blowing up serves as a fundamental technique in algebraic geometry for resolving singularities by replacing a point with an entire projective space, thereby transforming complex geometric structures into simpler, well-behaved forms. This process facilitates the study of algebraic varieties, enabling mathematicians to analyze and classify surfaces, curves, and higher-dimensional varieties with singular points. Applications of blowing up include the resolution of singularities in birational geometry, simplification of intersection theory, and construction of moduli spaces.
Advantages and Limitations of Desingularization
Desingularization offers a systematic approach to resolving singularities in algebraic varieties by producing smooth models, which enhances the ability to apply differential-geometric and topological methods. Its advantages include providing canonical resolutions that preserve the underlying structure, facilitating explicit calculations in birational geometry and moduli problems. However, desingularization can be computationally intensive, may not be unique in positive characteristic, and sometimes introduces complex intermediate spaces that complicate geometric interpretations.
Comparative Case Studies and Examples
Desingularization and blowing-up are resolution techniques used in algebraic geometry to handle singularities on algebraic varieties, with desingularization aiming to replace a singular variety with a smooth one via a proper birational morphism, while blowing-up introduces exceptional divisors at singular points to locally modify the variety's structure. Comparative case studies, such as resolving singular points on surfaces or curves, illustrate that blowing-up is often the first step in desingularization, providing explicit transformations that simplify singularities, as seen in the resolution of cusps or nodes. Examples including resolving singularities of plane curves highlight how blowing-up transforms complex singularities into simpler or smooth points, facilitating the iterative process toward full desingularization.
Modern Approaches in Singularity Resolution
Modern approaches in singularity resolution emphasize desingularization techniques that systematically replace singular points with simpler geometric structures to achieve smooth manifolds. Blowing up remains a fundamental operation, allowing precise local modifications by replacing singular loci with exceptional divisors, thereby improving the variety's structure. Advanced algorithms and computational algebraic geometry tools now integrate both methods to optimize resolution processes in complex algebraic varieties.
Future Directions in Algebraic Geometry Research
Future directions in algebraic geometry research emphasize enhancing desingularization algorithms to handle higher-dimensional varieties with more complex singularities, leveraging advancements in computational power and machine learning techniques. Blowing up remains a fundamental tool, with ongoing exploration into novel blowup schemes that optimize resolution efficiency and preserve geometric properties more effectively. Integration of these methods with derived algebraic geometry and Homological Mirror Symmetry offers promising pathways to unify singularity resolution frameworks and deepen understanding of moduli spaces.
Desingularization Infographic
 libterm.com
libterm.com