Baire space is a fundamental concept in topology and analysis, characterized by the property that the intersection of countably many dense open sets is dense. This space plays a vital role in understanding generic properties and has applications in functional analysis and descriptive set theory. Explore the rest of this article to discover how Baire space impacts various mathematical fields and your studies.
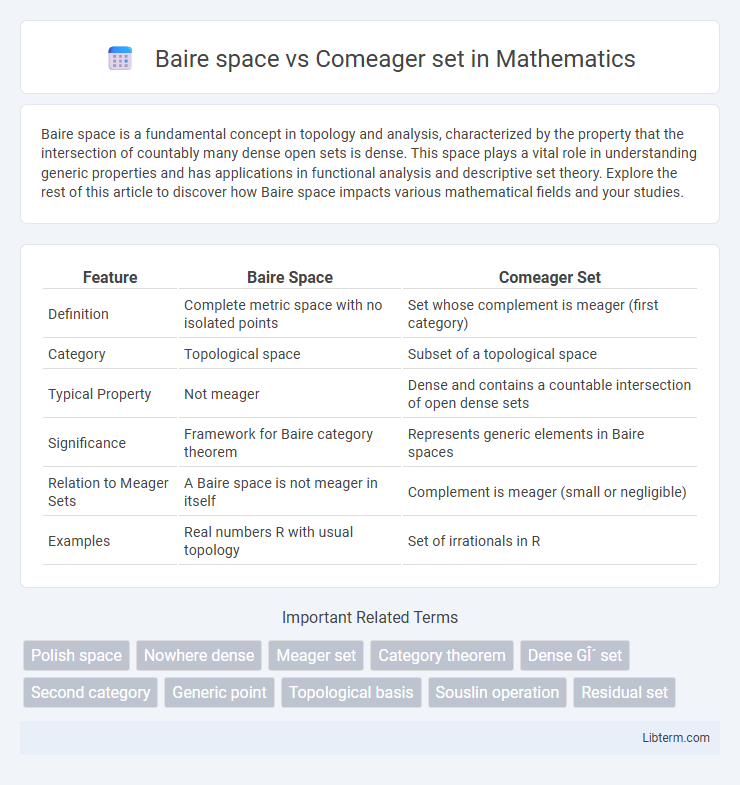
Table of Comparison
| Feature | Baire Space | Comeager Set |
|---|---|---|
| Definition | Complete metric space with no isolated points | Set whose complement is meager (first category) |
| Category | Topological space | Subset of a topological space |
| Typical Property | Not meager | Dense and contains a countable intersection of open dense sets |
| Significance | Framework for Baire category theorem | Represents generic elements in Baire spaces |
| Relation to Meager Sets | A Baire space is not meager in itself | Complement is meager (small or negligible) |
| Examples | Real numbers R with usual topology | Set of irrationals in R |
Introduction to Baire Space and Comeager Sets
Baire space, denoted by \(\omega^\omega\), is a fundamental object in descriptive set theory characterized as a Polish space that is completely metrizable and zero-dimensional, consisting of all infinite sequences of natural numbers. Comeager sets, also known as residual sets, are those containing a countable intersection of dense open sets in a topological space, thereby being "large" from the viewpoint of category theory. In Baire spaces, comeager sets form a crucial concept because they represent typical or generic properties, contrasting with meager (first category) sets, which are considered topologically small or negligible.
Definition of Baire Space
A Baire space is a topological space in which the intersection of countably many dense open sets is dense, ensuring that the space is not the union of countably many nowhere dense sets. In contrast, a comeager set is a subset whose complement is meager, meaning it can be expressed as a countable union of nowhere dense sets. The Baire category theorem guarantees that complete metric spaces and locally compact Hausdorff spaces are examples of Baire spaces, highlighting their structural robustness in terms of category.
Key Properties of Baire Spaces
Baire spaces are topological spaces where the intersection of countably many dense open sets remains dense, which ensures that they are not meager or "small" in terms of category. Key properties include the Baire category theorem stating that complete metric spaces and locally compact Hausdorff spaces are Baire spaces, making them robust frameworks for analysis and topology. Comeager sets are the complements of meager sets and are dense in Baire spaces, reflecting the notion that "large" subsets dominate the space's structure.
Definition of Comeager Sets
Comeager sets, also known as residual sets, are defined in the context of Baire spaces as sets whose complement is meager, meaning the complement can be expressed as a countable union of nowhere dense subsets. In a Baire space, comeager sets are dense by nature and their intersection is dense as well, highlighting their significance in topology and functional analysis. These sets play a crucial role in Baire category theorem applications, indicating typical or generic properties within complete metric spaces or locally compact Hausdorff spaces.
Essential Features of Comeager Sets
Comeager sets in Baire spaces are characterized by their countable intersection of dense open sets, making them topologically large and prevalent. These sets possess the Baire property, ensuring they are residual and their complements are meager, indicating "smallness" in category terms. The essential feature of comeager sets is their robustness under countable intersections and their role in genericity within complete metric or Baire spaces.
Comparison: Baire Space vs Comeager Set
Baire spaces are topological spaces where the intersection of countably many dense open sets remains dense, ensuring robustness against "small" subsets, while comeager sets are those whose complements are meager (first category), representing "large" or generic subsets in a Baire space. The core distinction lies in the context: Baire space is a property of the entire topological space ensuring non-meagerness of residual sets, whereas comeager sets are specific subsets characterized by being residual and thus topologically large within a Baire space. In essence, comeager sets exemplify the typical elements of a Baire space, highlighting the interplay between density, category, and topology.
Role of Baire Category Theorem
Baire space, a topological space where the Baire Category Theorem holds, ensures that the intersection of countably many dense open sets is dense, providing a framework to distinguish comeager (residual) sets from meager sets. Comeager sets, characterized as countable intersections of dense open sets, represent "large" subsets in Baire spaces and play a crucial role in descriptive set theory and functional analysis. The Baire Category Theorem guarantees that comeager sets are nonempty and dense, supporting continuity properties and genericity results in complete metric spaces and locally compact Hausdorff spaces.
Applications in Topology and Analysis
Baire spaces serve as a foundational concept in topology and analysis, ensuring that countable intersections of dense open sets remain dense, which supports robust genericity arguments. Comeager sets, defined as complements of meager (nowhere dense) sets, characterize "large" subsets in Baire spaces, often used in proving typical properties in functional analysis and dynamical systems. These concepts are instrumental in the study of generic properties of continuous functions, descriptive set theory, and the structural analysis of complete metric and locally compact spaces.
Common Examples and Counterexamples
Baire spaces are topological spaces where the intersection of countably many dense open sets remains dense, with the real numbers \(\mathbb{R}\) under the usual topology serving as a prime example. Comeager sets, defined as complements of meager (first category) sets, commonly appear in Baire spaces; for instance, the set of irrational numbers is comeager in \(\mathbb{R}\) because the rationals are meager. A notable counterexample arises in spaces without the Baire property, such as certain subspaces of \(\mathbb{Q}\), where comeager sets may fail to be dense or nonempty, illustrating the necessity of the Baire space condition for many classical results.
Summary and Further Reading
Baire space is a topological space where the intersection of countably many dense open sets remains dense, crucial for understanding comeager sets--sets containing a countable intersection of dense open subsets, making them "large" or generic in a topological sense. Comeager sets serve as the complement of meager (or "small") sets and play a pivotal role in descriptive set theory and functional analysis, especially in the context of Baire category theorem applications. For further reading, explore Oxtoby's "Measure and Category" and Kechris's "Classical Descriptive Set Theory," which delve deeper into the interplay between Baire spaces and comeager sets.
Baire space Infographic
 libterm.com
libterm.com