The net and lateral face of a three-dimensional shape provide key insights into its geometry and surface area. Understanding how the net unfolds helps visualize the shape's structure, while the lateral face reveals details about its sides excluding the base. Explore the rest of this article to deepen your grasp of these essential geometric concepts.
Table of Comparison
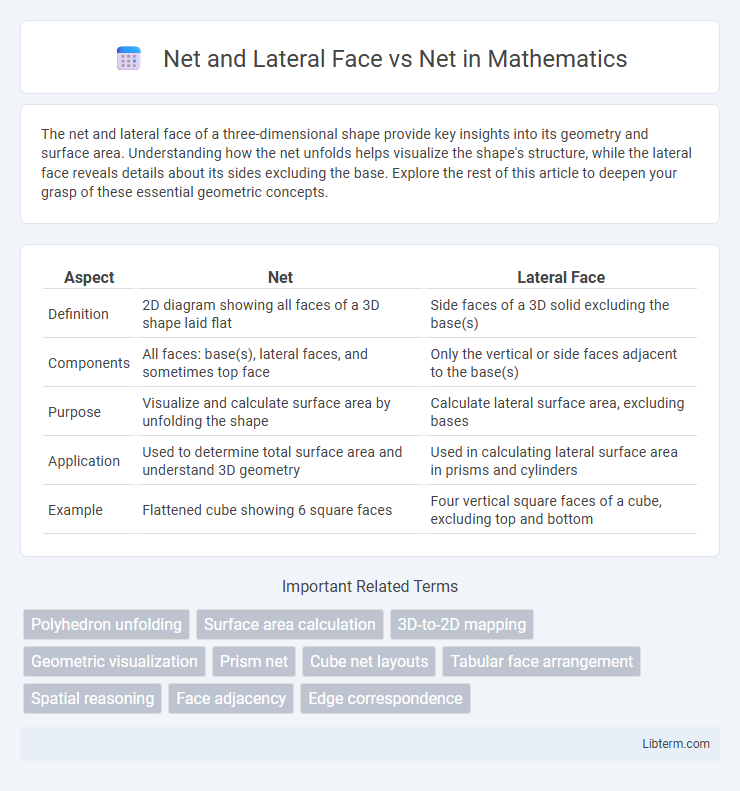
| Aspect | Net | Lateral Face |
|---|---|---|
| Definition | 2D diagram showing all faces of a 3D shape laid flat | Side faces of a 3D solid excluding the base(s) |
| Components | All faces: base(s), lateral faces, and sometimes top face | Only the vertical or side faces adjacent to the base(s) |
| Purpose | Visualize and calculate surface area by unfolding the shape | Calculate lateral surface area, excluding bases |
| Application | Used to determine total surface area and understand 3D geometry | Used in calculating lateral surface area in prisms and cylinders |
| Example | Flattened cube showing 6 square faces | Four vertical square faces of a cube, excluding top and bottom |
Understanding Geometric Nets: An Overview
Geometric nets are two-dimensional patterns that can be folded to form three-dimensional shapes, with the net representing all faces of the solid spread out flat. Understanding the relationship between the net and lateral faces is crucial, as the lateral faces make up the sides of a 3D shape excluding the base(s), which helps in visualizing and calculating surface areas accurately. Mastery of net construction aids in comprehending spatial structures, making it easier to solve problems involving volume and surface area in geometry.
What Is a Net in Geometry?
A net in geometry is a two-dimensional shape that can be folded to form a three-dimensional solid, revealing all its faces laid out flat. The lateral face refers specifically to the sides of a solid, excluding its base and top, which are also represented in the net. Understanding the net of a figure helps visualize how these lateral faces and bases fit together to create the solid's complete surface area.
Defining Lateral Faces and Their Importance
Lateral faces refer to the rectangular or parallelogram surfaces that connect the base of a three-dimensional solid, such as a prism or pyramid, to its apex or opposite side. These faces are crucial for calculating surface area and understanding the shape's overall geometry, as they represent the sides excluding the base(s). Recognizing lateral faces facilitates accurate modeling in fields like architecture and engineering by providing essential data for design and structural analysis.
Differences Between Net and Lateral Faces
Net and lateral face are key concepts in geometry related to 3D shapes. A net is a two-dimensional layout that, when folded, forms the entire 3D solid, showing all faces including the base and lateral faces. Lateral faces refer exclusively to the side surfaces of a 3D solid, excluding the base or bases, highlighting the main difference where the net represents the complete unfolded shape, while lateral faces pertain only to specific side areas of the solid.
Role of Lateral Faces within a Net
Lateral faces within a net play a crucial role in unfolding three-dimensional solids such as prisms and pyramids into two-dimensional diagrams, enabling accurate surface area calculations. These faces connect the base(s) and provide essential geometric details that contribute to the net's layout and overall structure. Understanding the lateral faces is key for visualizing solid dimensions and facilitating precise mathematical modeling.
Visualizing 3D Shapes: Net and Lateral Face Connections
Visualizing 3D shapes involves understanding the relationship between nets and lateral faces, where a net represents a two-dimensional pattern that can be folded to form the 3D shape. The lateral face consists of the sides connecting the bases of prisms or cylinders, crucial for accurately assembling the net into its spatial structure. Mastery of lateral face identification within nets enhances spatial reasoning and facilitates the comprehension of complex three-dimensional objects.
Applications of Nets and Lateral Faces in Real Life
Nets simplify the construction and visualization of three-dimensional shapes by unfolding them into two-dimensional patterns, essential for packaging design, manufacturing, and architectural modeling. Lateral faces, the vertical sides of prisms and cylinders, play a crucial role in calculating surface areas for materials estimation in real-world applications like constructing tanks, silos, and shipping containers. Understanding nets and lateral faces enables precise fabrication and cost-effective use of materials across engineering, design, and industrial processes.
How to Identify Lateral Faces in a Net
To identify lateral faces in a net of a three-dimensional solid, look for the rectangles or parallelograms that connect the base to the top face, usually forming the sides of the solid. Unlike the base or top face, which are often polygonal and lie flat in the net, lateral faces are adjacent and aligned vertically or along the edges connecting bases. Recognizing the lateral faces is key in understanding the solid's surface area and three-dimensional structure.
Common Geometric Shapes and Their Nets
Common geometric shapes like cubes, pyramids, and prisms have nets that unfold their lateral faces into two-dimensional patterns. The lateral face of a shape refers to the sides excluding the base, which when laid flat create part of the net. Understanding the net of a shape helps visualize 3D structures and calculate surface areas by relating the lateral faces and bases in their unfolded forms.
Tips for Teaching Nets and Lateral Faces
Teaching nets and lateral faces effectively demands clear visual aids and hands-on activities to help students grasp 3D shapes. Use color-coding to differentiate between nets and lateral faces, emphasizing how nets fold into solids and how lateral faces form the sides of prisms and cylinders. Incorporate real-life objects to link abstract concepts to tangible experiences, enhancing comprehension and retention of geometric properties.
Net and Lateral Face Infographic
 libterm.com
libterm.com