The Wu formula is a mathematical method used to calculate the contribution of each expert in a group decision-making process, optimizing the weighting of opinions. This technique ensures your decisions are data-driven and accurately reflect the expertise of all participants. Explore the rest of the article to understand how the Wu formula can enhance your collaborative evaluations.
Table of Comparison
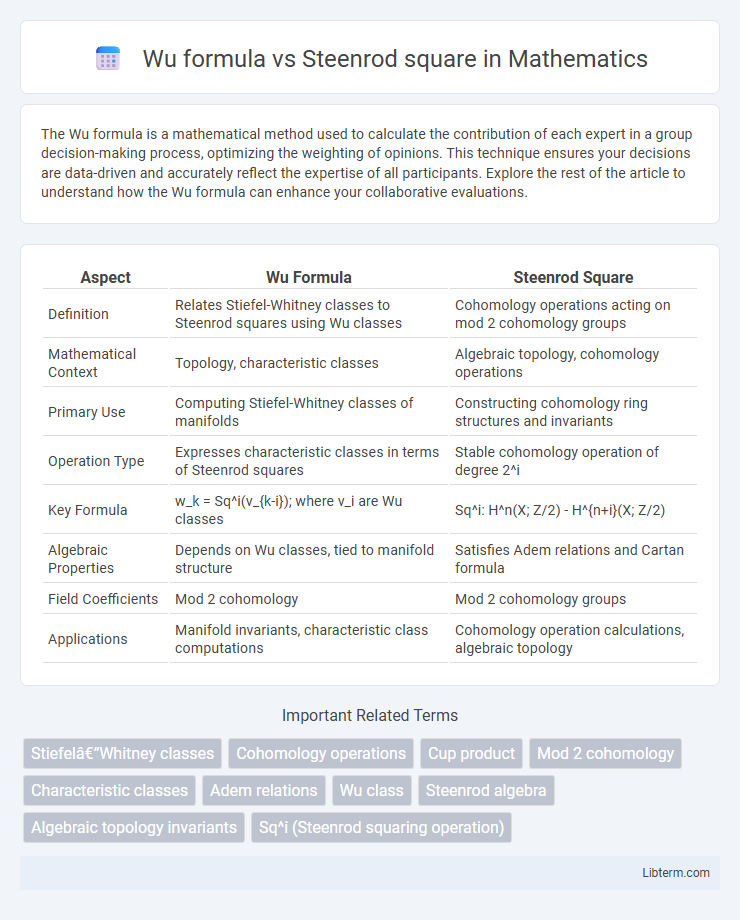
| Aspect | Wu Formula | Steenrod Square |
|---|---|---|
| Definition | Relates Stiefel-Whitney classes to Steenrod squares using Wu classes | Cohomology operations acting on mod 2 cohomology groups |
| Mathematical Context | Topology, characteristic classes | Algebraic topology, cohomology operations |
| Primary Use | Computing Stiefel-Whitney classes of manifolds | Constructing cohomology ring structures and invariants |
| Operation Type | Expresses characteristic classes in terms of Steenrod squares | Stable cohomology operation of degree 2^i |
| Key Formula | w_k = Sq^i(v_{k-i}); where v_i are Wu classes | Sq^i: H^n(X; Z/2) - H^{n+i}(X; Z/2) |
| Algebraic Properties | Depends on Wu classes, tied to manifold structure | Satisfies Adem relations and Cartan formula |
| Field Coefficients | Mod 2 cohomology | Mod 2 cohomology groups |
| Applications | Manifold invariants, characteristic class computations | Cohomology operation calculations, algebraic topology |
Introduction to Wu Formula and Steenrod Square
Wu formula connects Stiefel-Whitney classes to Steenrod squares, providing a tool to compute characteristic classes of smooth manifolds. Steenrod squares are cohomology operations in mod 2 cohomology, crucial for manipulating and analyzing topological spaces. The Wu formula leverages Steenrod squares to relate characteristic classes, enabling explicit calculations in algebraic topology.
Historical Background and Development
The Wu formula, introduced by Wu Wenjun in the 1950s, established a foundational relationship between Steenrod squares and Stiefel-Whitney classes in algebraic topology. Steenrod squares, developed earlier by Norman Steenrod in the 1940s, are cohomology operations that act on mod 2 cohomology, forming a basis for the study of characteristic classes. Together, these tools significantly advanced the understanding of manifold invariants and paved the way for modern topological insights.
Mathematical Foundations of Wu Formula
Wu formula arises from the intersection of algebraic topology and cohomology theory, establishing a crucial link between Stiefel-Whitney classes and Steenrod squares. It provides a method to express Stiefel-Whitney classes in terms of Steenrod squares applied to dual homology classes, enhancing the computation in characteristic classes of manifolds. The key mathematical foundation involves identifying Steenrod square operations as stable cohomology operations that satisfy specific axioms, enabling the derivation of secondary cohomology invariants encoded by the Wu formula.
Understanding Steenrod Squares
Steenrod squares are cohomology operations in algebraic topology that act on the cohomology groups with mod 2 coefficients, providing a powerful tool to detect nontrivial topological structures. Wu's formula establishes a fundamental relationship between Steenrod squares and Stiefel-Whitney classes, showing how specific Steenrod square operations correspond to the characteristic classes of manifolds. Understanding Steenrod squares enables deeper insights into the algebraic invariants of topological spaces, bridging the gap between homology, cohomology, and manifold theory.
Relationship Between Wu Formula and Steenrod Squares
The Wu formula establishes a direct connection between Wu classes and Steenrod squares by expressing the action of Steenrod squares on cohomology classes through Wu classes. This relationship enables computation of Steenrod square operations via the formula Sqi = Wu_j x^{i-j}, linking algebraic topology invariants with characteristic classes. Understanding this interplay is crucial in the study of manifold invariants and mod 2 cohomology operations.
Applications in Algebraic Topology
Wu formulas provide a method to calculate Stiefel-Whitney classes of manifolds by relating these characteristic classes to Steenrod squares acting on cohomology classes. Steenrod squares, as stable cohomology operations, play a crucial role in detecting the nontriviality of cohomology classes and enable computations in the cohomology ring of topological spaces. These tools are essential in classifying vector bundles, analyzing manifold invariants, and studying cobordism theory within algebraic topology.
Computational Techniques for Wu Formula
Computational techniques for the Wu formula leverage the relationship between characteristic classes and Steenrod squares, enabling efficient calculation of Stiefel-Whitney classes in algebraic topology. By expressing Wu classes through Steenrod square operations, algorithms can systematically compute cohomology operations on manifolds, facilitating practical applications in topology and geometry. Implementations often utilize chain-level approximations and cochain complexes to optimize the calculation of Wu classes in complex spaces.
Key Properties of Steenrod Squares
Steenrod squares are stable cohomology operations defined on mod 2 cohomology classes, satisfying naturality, dimension constraints, and Cartan formula, which governs their behavior with respect to cup products. They exhibit Adem relations that provide algebraic relations among compositions of Steenrod squares, enabling efficient computations in the Steenrod algebra. Wu formula connects Stiefel-Whitney classes and Steenrod squares by expressing the Stiefel-Whitney classes as specific Steenrod square operations on the Wu classes of a manifold.
Comparing Strengths and Limitations
Wu formula provides explicit relations between Stiefel-Whitney classes and Steenrod squares, enabling concrete computations in characteristic class theory. Steenrod squares offer a broad algebraic framework for cohomology operations over mod 2 coefficients, applicable in diverse topological contexts but often abstract and computationally intensive. While Wu formula excels in practical calculations within smooth manifold theory, Steenrod squares possess greater generality and algebraic depth, though they may lack direct geometric interpretations.
Conclusion: Choosing Between Wu Formula and Steenrod Squares
Selecting between the Wu formula and Steenrod squares depends on the computational context within algebraic topology and cohomology operations. The Wu formula provides an efficient way to calculate characteristic classes via Wu classes, particularly useful in differential topology and the study of manifolds. Steenrod squares offer a more general framework for cohomology operations with applications in homotopy theory and algebraic geometry, allowing deeper analysis of mod 2 cohomology rings.
Wu formula Infographic
 libterm.com
libterm.com