Associative memory enhances your ability to link related concepts, improving information retention and recall by creating meaningful connections. This cognitive process supports efficient learning and problem-solving by organizing data into interconnected networks. Explore the rest of the article to understand how associative techniques can boost your mental performance.
Table of Comparison
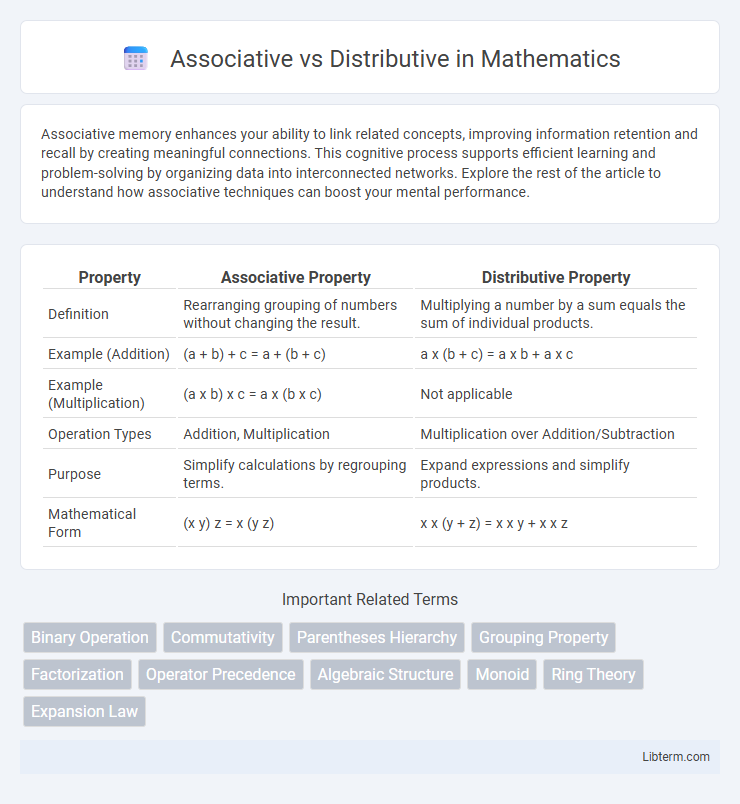
| Property | Associative Property | Distributive Property |
|---|---|---|
| Definition | Rearranging grouping of numbers without changing the result. | Multiplying a number by a sum equals the sum of individual products. |
| Example (Addition) | (a + b) + c = a + (b + c) | a x (b + c) = a x b + a x c |
| Example (Multiplication) | (a x b) x c = a x (b x c) | Not applicable |
| Operation Types | Addition, Multiplication | Multiplication over Addition/Subtraction |
| Purpose | Simplify calculations by regrouping terms. | Expand expressions and simplify products. |
| Mathematical Form | (x y) z = x (y z) | x x (y + z) = x x y + x x z |
Understanding Associative and Distributive Properties
The associative property in mathematics refers to the grouping of numbers without changing their sum or product, such as (a + b) + c = a + (b + c) for addition and (a x b) x c = a x (b x c) for multiplication. The distributive property involves multiplying a single term across terms inside a parenthesis, expressed as a x (b + c) = a x b + a x c, combining multiplication and addition operations. Understanding these properties is essential for simplifying expressions and solving algebraic problems efficiently.
Defining the Associative Property
The associative property defines how numbers can be grouped when added or multiplied without changing the result, expressed as (a + b) + c = a + (b + c) for addition and (a x b) x c = a x (b x c) for multiplication. This property highlights that the grouping of operands does not affect the outcome in both addition and multiplication operations. Understanding the associative property is essential in simplifying complex algebraic expressions and optimizing computational processes.
Examples of the Associative Property in Mathematics
The associative property in mathematics states that the grouping of numbers does not affect the result of addition or multiplication, such as (2 + 3) + 4 = 2 + (3 + 4) for addition and (2 x 3) x 4 = 2 x (3 x 4) for multiplication. This property is crucial when simplifying expressions because it allows for flexible regrouping without changing the outcome. An example in algebra is (x + y) + z = x + (y + z), demonstrating consistent sums regardless of parentheses placement.
Defining the Distributive Property
The distributive property states that multiplying a number by a sum equals the sum of the individual products, expressed as a(b + c) = ab + ac. This property allows for the extension of multiplication over addition or subtraction within parentheses, facilitating algebraic simplification and problem solving. Unlike the associative property, which deals with regrouping numbers, the distributive property connects multiplication and addition operations.
Examples of the Distributive Property in Action
The distributive property demonstrates how multiplication distributes over addition or subtraction, such as in 3 x (4 + 5) = 3 x 4 + 3 x 5 = 12 + 15 = 27. Another example includes applying the property to algebraic expressions: a(b + c) = ab + ac, like 2(x + 7) = 2x + 14. These examples highlight the efficiency of the distributive property in simplifying expressions and solving equations.
Key Differences Between Associative and Distributive Properties
The key differences between associative and distributive properties lie in their operational focus and structure: the associative property applies to grouping of numbers in addition or multiplication without changing the order, such as (a + b) + c = a + (b + c), while the distributive property connects multiplication and addition, allowing terms to be multiplied separately before summing, shown as a x (b + c) = a x b + a x c. Associative property emphasizes how operands are grouped, whereas distributive property illustrates how multiplication distributes over addition or subtraction. Both properties are fundamental in simplifying algebraic expressions and solving equations efficiently.
Real-Life Applications of Associative and Distributive Laws
The associative law simplifies complex calculations by allowing the grouping of numbers in addition and multiplication, which is essential in computer algorithms and mental math strategies for efficiency. The distributive law enables breaking down expressions to simplify multiplication over addition or subtraction, playing a crucial role in algebraic problem solving and financial calculations such as interest computations. Both laws are fundamental in programming, engineering, and economics for optimizing operations and ensuring accurate results in resource allocation and data processing.
Common Mistakes When Using These Properties
Common mistakes when using associative and distributive properties include incorrectly grouping terms or misapplying the operation order, such as assuming distributive applies to addition inside parentheses without multiplication outside. Confusing the associative property of addition or multiplication with distributive property leads to errors, especially when variables and constants are combined. Another frequent error is overlooking the need to apply the distributive property to every term inside the parentheses, resulting in incomplete or incorrect expressions.
Why Associative and Distributive Properties Matter in Algebra
Associative and distributive properties matter in algebra because they provide foundational rules that simplify complex expressions and solve equations more efficiently. The associative property allows for the regrouping of numbers in addition or multiplication without changing the result, enabling flexible computation and easier mental math. The distributive property connects multiplication and addition, allowing expressions to be expanded or factored, which is essential for solving linear equations and simplifying polynomial expressions.
Quick Tips for Mastering Associative vs Distributive Properties
Mastery of associative and distributive properties hinges on recognizing operation grouping and distribution of multiplication over addition or subtraction. Use quick tips such as grouping numbers with parentheses for associative property (e.g., (a + b) + c = a + (b + c)) and expanding expressions by multiplying each term inside parentheses for distributive property (e.g., a(b + c) = ab + ac). Practicing these techniques with varied numerical and algebraic examples enhances speed and accuracy in simplifying expressions.
Associative Infographic
 libterm.com
libterm.com