Quotient is a mathematical term representing the result of division between two numbers, indicating how many times one number fits into another. Understanding quotients is essential for solving problems involving fractions, ratios, and algebraic expressions. Explore the rest of the article to deepen your grasp of how quotients function in various mathematical contexts.
Table of Comparison
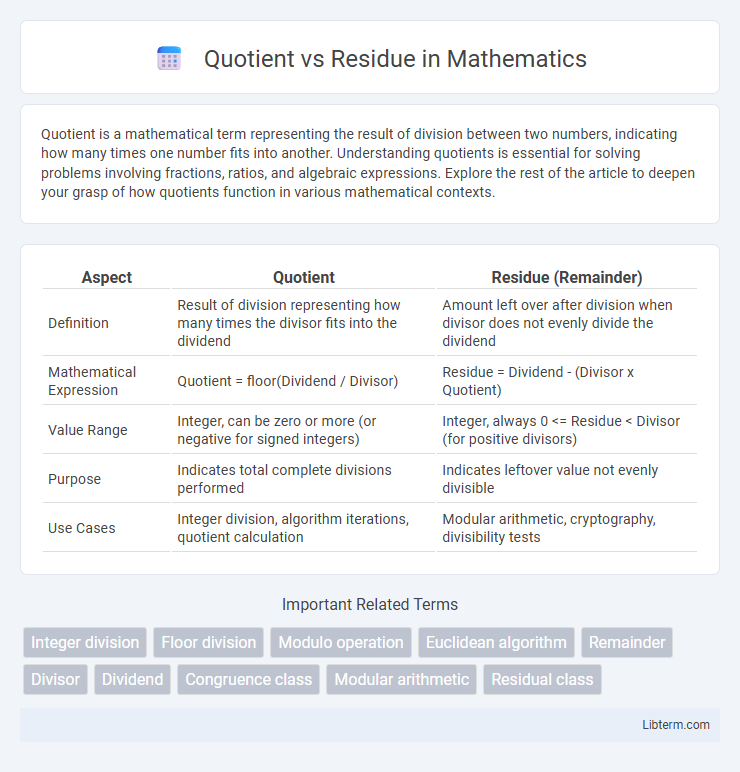
| Aspect | Quotient | Residue (Remainder) |
|---|---|---|
| Definition | Result of division representing how many times the divisor fits into the dividend | Amount left over after division when divisor does not evenly divide the dividend |
| Mathematical Expression | Quotient = floor(Dividend / Divisor) | Residue = Dividend - (Divisor x Quotient) |
| Value Range | Integer, can be zero or more (or negative for signed integers) | Integer, always 0 <= Residue < Divisor (for positive divisors) |
| Purpose | Indicates total complete divisions performed | Indicates leftover value not evenly divisible |
| Use Cases | Integer division, algorithm iterations, quotient calculation | Modular arithmetic, cryptography, divisibility tests |
Understanding Quotient and Residue
The quotient represents the integer result of division, showing how many times the divisor fully fits into the dividend. The residue, or remainder, is the leftover part of the dividend after dividing by the divisor, smaller than the divisor itself. Understanding the quotient and residue is essential for problems involving modular arithmetic, division algorithms, and number theory.
Definitions: What Is a Quotient?
A quotient is the result obtained when one number, called the dividend, is divided by another number, called the divisor. It represents how many times the divisor fits into the dividend without considering the remainder. In division operations, the quotient quantifies the complete sets formed by the divisor within the dividend.
Definitions: What Is a Residue?
A residue is the remainder left after dividing one integer by another in modular arithmetic, often denoted as the remainder in the expression \(a = bq + r\), where \(a\) is the dividend, \(b\) is the divisor, \(q\) is the quotient, and \(r\) is the residue. The residue represents the smallest non-negative integer value \(r\) such that \(0 \leq r < b\). Understanding residues is crucial in number theory, cryptography, and computer science algorithms involving modular operations.
Mathematical Representation of Quotient and Residue
The quotient in division represents the number of times the divisor fits completely into the dividend, mathematically expressed as \( q = \lfloor \frac{a}{b} \rfloor \) where \( a \) is the dividend and \( b \) is the divisor. The residue, or remainder, is defined as the difference between the dividend and the product of the divisor and the quotient, represented by \( r = a - bq \), satisfying \( 0 \leq r < b \). These equations form the fundamental basis of the division algorithm in number theory, ensuring precise decomposition of integers.
Steps to Calculate Quotient and Residue
To calculate the quotient and residue from a division operation, first divide the dividend by the divisor to determine how many whole times the divisor fits into the dividend, which gives the quotient. Then, multiply the quotient by the divisor and subtract this product from the dividend to find the residue (remainder). These steps ensure accurate division results represented as dividend = (quotient x divisor) + residue.
Real-Life Applications of Quotient and Residue
Quotient and residue play vital roles in real-life applications such as cryptography, where quotient operations enable modular arithmetic crucial for encryption algorithms, and residues ensure data integrity through checksums. In computer science, quotient calculations manage data partitioning and storage optimization, while residues assist in error detection and correction processes. Financial modeling relies on quotients for interest rate calculations, and residues help in balancing accounts and distributing divisible assets.
Key Differences Between Quotient and Residue
The quotient represents the number of times a divisor fits completely into a dividend during division, while the residue (or remainder) is the leftover part that cannot be evenly divided. Quotient is always an integer result of division, whereas residue can range from zero up to one less than the divisor. Understanding these key differences is essential for applications in modular arithmetic, computer science algorithms, and number theory.
Visual Examples: Quotient vs Residue
In division, the quotient represents the number of times the divisor fits completely into the dividend, while the residue (or remainder) is the part left over after this division. For example, dividing 17 by 5 yields a quotient of 3 because 5 fits three full times into 17, and a residue of 2 since 17 minus (5 times 3) equals 2. Visualizing this, if 17 objects are grouped into piles of 5, three full piles are made (quotient), and 2 objects remain ungrouped (residue).
Common Mistakes in Differentiating Quotient and Residue
Common mistakes in differentiating quotient and residue often arise from confusing the division result with the remainder in modular arithmetic. Quotient refers to the integer outcome of division, ignoring any fractional or leftover part, while residue specifically denotes the remainder left after division. Misinterpreting these terms can lead to errors in algorithm design, number theory problems, and computer programming involving modular operations.
Summary Table: Quotient vs Residue
The summary table comparing Quotient vs Residue highlights that the quotient represents the result of division, indicating how many times the divisor fits entirely into the dividend, while the residue (or remainder) shows the leftover value that cannot be evenly divided. In arithmetic and modular arithmetic, the quotient is integral in determining the division's magnitude, whereas the residue is crucial for understanding modular equivalence classes or leftover quantities. This distinction is vital in applications like computer algorithms, cryptography, and number theory where precise division outcomes and remainders influence calculations and problem-solving strategies.
Quotient Infographic
 libterm.com
libterm.com