Deductive reasoning involves drawing specific conclusions from general premises, ensuring that if the premises are true, the conclusion must be true as well. This logical process is fundamental in fields such as mathematics, law, and science, where establishing certainty is crucial. Explore the rest of the article to deepen your understanding of how deductive reasoning can enhance your critical thinking skills.
Table of Comparison
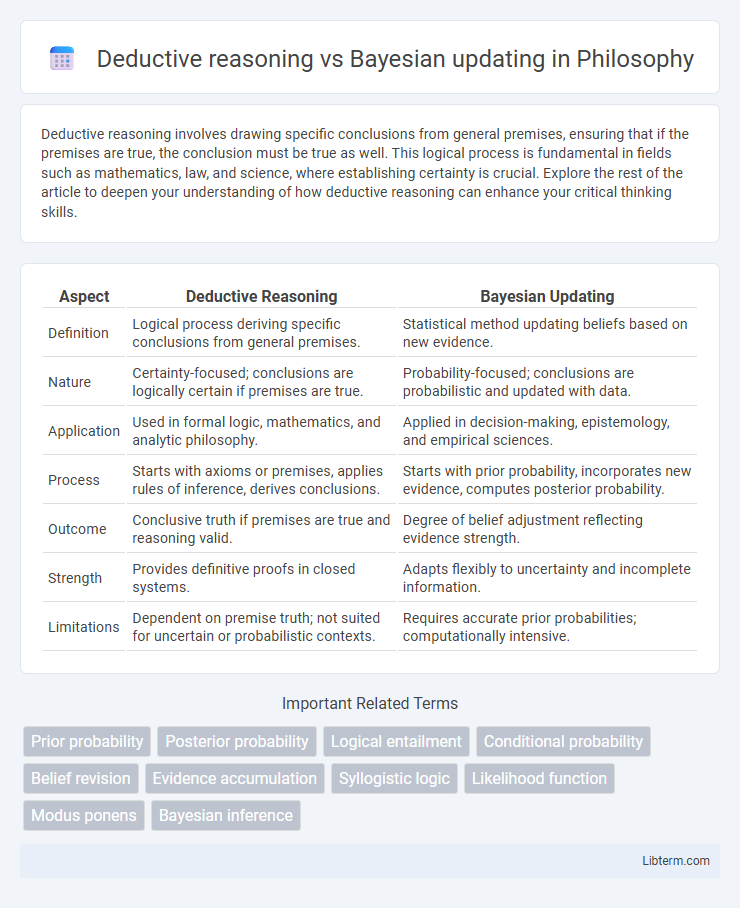
| Aspect | Deductive Reasoning | Bayesian Updating |
|---|---|---|
| Definition | Logical process deriving specific conclusions from general premises. | Statistical method updating beliefs based on new evidence. |
| Nature | Certainty-focused; conclusions are logically certain if premises are true. | Probability-focused; conclusions are probabilistic and updated with data. |
| Application | Used in formal logic, mathematics, and analytic philosophy. | Applied in decision-making, epistemology, and empirical sciences. |
| Process | Starts with axioms or premises, applies rules of inference, derives conclusions. | Starts with prior probability, incorporates new evidence, computes posterior probability. |
| Outcome | Conclusive truth if premises are true and reasoning valid. | Degree of belief adjustment reflecting evidence strength. |
| Strength | Provides definitive proofs in closed systems. | Adapts flexibly to uncertainty and incomplete information. |
| Limitations | Dependent on premise truth; not suited for uncertain or probabilistic contexts. | Requires accurate prior probabilities; computationally intensive. |
Introduction to Deductive Reasoning and Bayesian Updating
Deductive reasoning involves drawing logically certain conclusions from general premises, ensuring that if the premises are true, the conclusion must be true. Bayesian updating refines probability estimates by incorporating new evidence according to Bayes' theorem, allowing for dynamic adjustment of beliefs based on observed data. Both methods serve critical roles in decision-making, with deductive reasoning providing definitive conclusions and Bayesian updating offering probabilistic insights.
Defining Deductive Reasoning
Deductive reasoning involves deriving specific conclusions from general premises with logical certainty, ensuring that if the premises are true, the conclusion must be true. It relies on formal logic structures such as syllogisms and modus ponens to establish valid inferences. This method contrasts with Bayesian updating, which probabilistically adjusts beliefs based on new evidence rather than guaranteeing absolute certainty.
Core Concepts of Bayesian Updating
Bayesian updating revolves around revising prior probabilities based on new evidence, encapsulated by Bayes' theorem, which mathematically formulates posterior probability as a product of prior probability and likelihood of observed data. Unlike deductive reasoning that derives conclusions with certainty from premises, Bayesian updating manages uncertainty by continuously refining belief distributions with incoming information. This probabilistic approach underpins decision making in fields such as machine learning, statistics, and cognitive science by quantifying the impact of evidence on hypotheses.
Key Differences Between Deductive and Bayesian Approaches
Deductive reasoning relies on definitive logical conclusions drawn from general premises, ensuring absolute certainty when premises are true. Bayesian updating, in contrast, deals with probabilistic inference, adjusting beliefs based on new evidence and prior probabilities. The key difference lies in deductive reasoning's use of fixed rules for undeniable conclusions versus Bayesian updating's flexible, data-driven probability revisions.
Logical Foundations: Certainty vs. Probability
Deductive reasoning operates on logical foundations that guarantee certainty, producing conclusions that must be true if the premises are true. Bayesian updating, grounded in probability theory, modifies beliefs by quantifying uncertainty and incorporating new evidence to revise the probability of hypotheses. The core distinction lies in deductive reasoning's absolute truth values versus Bayesian updating's probabilistic degrees of belief.
Real-World Applications of Deductive Reasoning
Deductive reasoning plays a crucial role in real-world applications such as diagnostic processes in medicine, where specific symptoms logically lead to a definitive diagnosis based on established medical principles. In legal contexts, deductive logic helps assess evidence and apply statutory laws to reach conclusive judgments. Engineering problem-solving frequently relies on deductive methods to design systems that meet predetermined specifications by logically deriving solutions from fundamental scientific laws.
Use Cases for Bayesian Updating
Bayesian updating excels in dynamic environments where prior knowledge integrates with new evidence, such as medical diagnosis, finance, and machine learning. It enables continuous probability revision, improving decision-making accuracy in uncertain scenarios like predicting stock market trends or updating spam filters. Unlike deductive reasoning's fixed premises, Bayesian updating adapts models based on real-time data for more flexible inference.
Strengths and Limitations of Each Method
Deductive reasoning excels in providing logically certain conclusions from given premises, making it highly reliable for formal proofs and structured problem-solving but often struggles with uncertainty and incomplete information. Bayesian updating offers a flexible framework for revising probabilities based on new evidence, supporting decision-making under uncertainty, yet it depends heavily on the accuracy of prior probabilities and computational complexity can increase with data size. Balancing these methods allows combining the rigidity of deductive logic with the adaptability of probabilistic inference for more robust reasoning systems.
Integrating Deductive and Bayesian Methods
Integrating deductive reasoning and Bayesian updating enhances decision-making by combining logical certainty with probabilistic evidence assessment. Deductive reasoning provides a structured framework for deriving conclusions from established premises, while Bayesian updating continuously refines the probability of hypotheses based on new data. This hybrid approach improves the robustness of inferences in complex scenarios by leveraging formal logic and dynamic belief revision simultaneously.
Choosing the Right Approach for Decision-Making
Deductive reasoning provides certainty by applying general principles to reach specific conclusions, making it ideal for decisions based on established rules or facts. Bayesian updating offers flexibility by incorporating new evidence probabilistically, which suits dynamic environments with uncertain or evolving information. Selecting the right approach depends on the decision context: use deductive reasoning when situations are well-defined and data is complete, while Bayesian updating excels in adapting beliefs and guiding decisions under uncertainty.
Deductive reasoning Infographic
 libterm.com
libterm.com