Propositional logic is a fundamental branch of logic that deals with propositions and their relationships using logical connectives such as AND, OR, and NOT. It serves as the foundation for developing algorithms, solving logical problems, and artificial intelligence applications. Explore the rest of this article to deepen your understanding of propositional logic's principles and its practical uses.
Table of Comparison
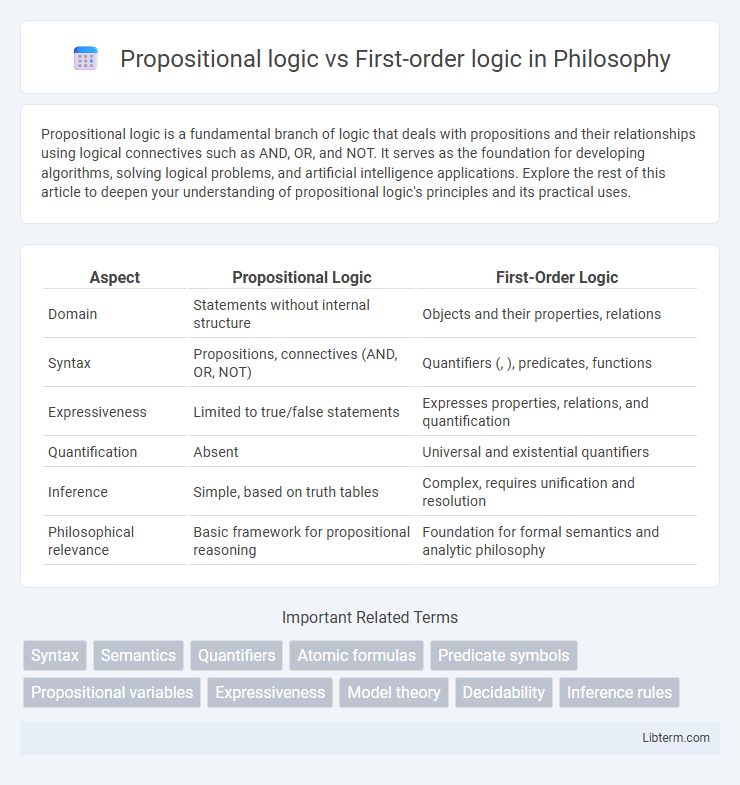
| Aspect | Propositional Logic | First-Order Logic |
|---|---|---|
| Domain | Statements without internal structure | Objects and their properties, relations |
| Syntax | Propositions, connectives (AND, OR, NOT) | Quantifiers (, ), predicates, functions |
| Expressiveness | Limited to true/false statements | Expresses properties, relations, and quantification |
| Quantification | Absent | Universal and existential quantifiers |
| Inference | Simple, based on truth tables | Complex, requires unification and resolution |
| Philosophical relevance | Basic framework for propositional reasoning | Foundation for formal semantics and analytic philosophy |
Introduction to Propositional Logic and First-Order Logic
Propositional logic deals with propositions as whole units and uses logical connectives such as AND, OR, and NOT to form compound statements, enabling reasoning about truth values without considering internal structure. First-order logic extends propositional logic by incorporating quantifiers like "forall" () and "exists" (), variables, and predicates that express properties and relationships between objects within a domain. The introduction to propositional logic establishes the foundation for understanding logic syntax and semantics, while first-order logic introduces a more expressive language essential for formalizing mathematics, computer science, and artificial intelligence.
Core Concepts of Propositional Logic
Propositional logic centers on variables representing simple, declarative propositions that are either true or false, using logical connectives such as AND, OR, NOT, and IMPLIES to form complex statements. It focuses on the truth-functional relationships between whole propositions without delving into internal structures or quantifiers. This contrasts with first-order logic, which extends propositional logic by including quantifiers and predicates allowing analysis of objects and their properties within a domain.
Core Concepts of First-Order Logic
First-order logic extends propositional logic by incorporating quantifiers, variables, and predicates, enabling expressions about objects and their properties within a domain. Core concepts include universal quantification () and existential quantification (), which allow statements about all or some elements in the domain, respectively. Unlike propositional logic, first-order logic supports relations among objects, making it essential for formal reasoning in mathematics, computer science, and artificial intelligence.
Syntax Differences: Propositional vs First-Order Logic
Propositional logic syntax consists of atomic propositions represented by symbols and logical connectives such as AND, OR, NOT, and IMPLIES, without internal structure within propositions. First-order logic syntax includes predicates applied to terms, variables, constants, functions, and quantifiers like FOR ALL () and EXISTS (), enabling expression about objects and their relationships. The presence of quantifiers and variable bindings in first-order logic distinguishes its syntax from the simpler, variable-free atomic propositions of propositional logic.
Expressive Power Comparison
Propositional logic is limited to expressing relationships between fixed, concrete propositions without internal structure, restricting its ability to represent complex statements involving objects or their properties. First-order logic extends this capacity by incorporating quantifiers and predicates, enabling the expression of statements about infinite domains and detailed relationships between objects. This enhanced expressive power makes first-order logic essential for formalizing mathematics, computer science, and natural language semantics beyond the capabilities of propositional logic.
Applications in Computer Science and AI
Propositional logic is extensively applied in computer science for circuit design, model checking, and automated theorem proving, where its simplicity allows efficient algorithms for satisfiability and verification problems. First-order logic, with its expressiveness in handling quantifiers and relations, underpins knowledge representation, natural language processing, and reasoning systems in artificial intelligence, enabling more complex inference and ontology modeling. The choice between propositional and first-order logic depends on the required expressiveness and computational complexity in AI applications such as expert systems and machine learning frameworks.
Limitations of Propositional Logic
Propositional logic is limited by its inability to express relationships between objects or quantify over them, making it insufficient for representing complex statements involving variables and predicates. Unlike first-order logic, propositional logic cannot handle statements like "All humans are mortal" or "There exists an x such that x is a prime number." This limitation restricts propositional logic to simple true/false propositions without the expressive power needed for more detailed reasoning in mathematics, computer science, and artificial intelligence.
Advantages of First-Order Logic
First-order logic offers greater expressive power than propositional logic by allowing quantifiers and predicates that can represent relationships between objects, enabling more detailed and complex statements. It supports variables and functions, facilitating the modeling of real-world scenarios more effectively in fields like artificial intelligence and mathematics. This enhanced expressiveness makes first-order logic essential for formal verification, automated theorem proving, and knowledge representation, where propositional logic's limited scope is insufficient.
Translating Problems Between the Logics
Translating problems from propositional logic to first-order logic enables the representation of more complex relationships by introducing quantifiers and predicates, which propositional logic lacks. Propositional logic treats statements as atomic units without internal structure, while first-order logic decomposes these statements into objects and properties, allowing finer-grained modeling of real-world scenarios. This translation often involves encoding propositional variables as ground predicates, facilitating the application of first-order inference techniques to problems originally expressed in propositional terms.
Summary and Key Takeaways
Propositional logic deals with simple, declarative statements evaluated as true or false without internal structure, while first-order logic extends this by incorporating quantifiers and predicates to express relations among objects. Key takeaways include that first-order logic offers greater expressive power for modeling complex statements involving variables and relationships, whereas propositional logic is limited to basic truth-functional operations. Consequently, first-order logic is fundamental in fields like mathematics and computer science for formal reasoning and automated theorem proving.
Propositional logic Infographic
 libterm.com
libterm.com