Modal logic explores necessity and possibility through operators expressing concepts like "necessarily" and "possibly," offering a robust framework for formal reasoning beyond classical logic. It is widely applied in fields such as philosophy, computer science, and linguistics to analyze statements involving knowledge, belief, and obligation. Discover how modal logic can deepen your understanding of complex logical structures by reading the full article.
Table of Comparison
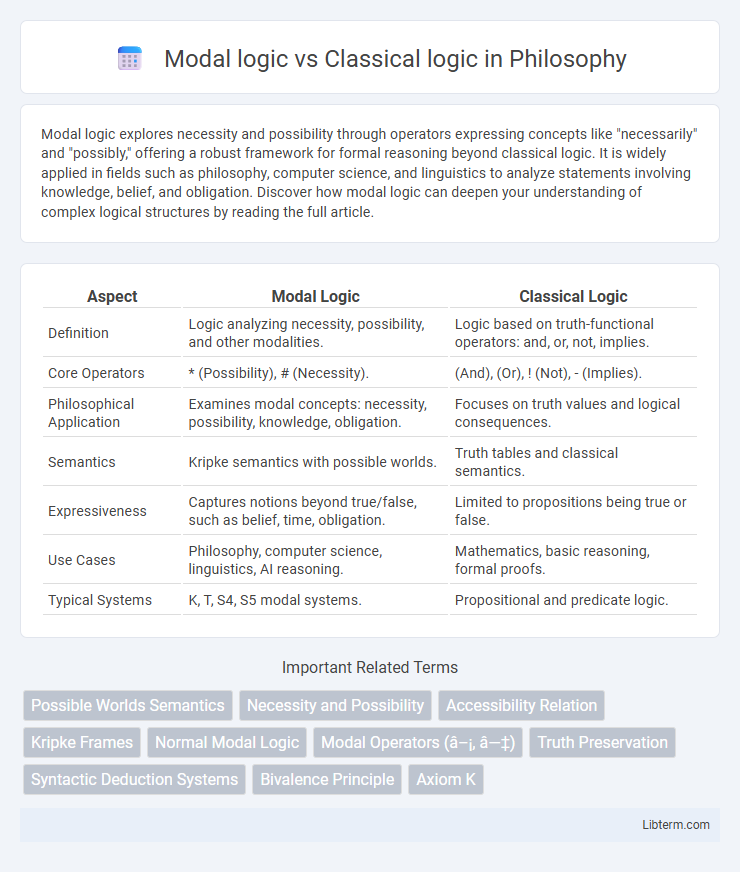
| Aspect | Modal Logic | Classical Logic |
|---|---|---|
| Definition | Logic analyzing necessity, possibility, and other modalities. | Logic based on truth-functional operators: and, or, not, implies. |
| Core Operators | * (Possibility), # (Necessity). | (And), (Or), ! (Not), - (Implies). |
| Philosophical Application | Examines modal concepts: necessity, possibility, knowledge, obligation. | Focuses on truth values and logical consequences. |
| Semantics | Kripke semantics with possible worlds. | Truth tables and classical semantics. |
| Expressiveness | Captures notions beyond true/false, such as belief, time, obligation. | Limited to propositions being true or false. |
| Use Cases | Philosophy, computer science, linguistics, AI reasoning. | Mathematics, basic reasoning, formal proofs. |
| Typical Systems | K, T, S4, S5 modal systems. | Propositional and predicate logic. |
Introduction to Modal Logic and Classical Logic
Modal logic extends classical logic by incorporating modalities expressing necessity and possibility, enabling reasoning about statements beyond simple true or false values. Classical logic relies on two-valued truth functions and fundamental principles such as the law of excluded middle and non-contradiction, forming the basis for propositional and predicate logic. Modal logic introduces operators like * (possibly) and # (necessarily), enriching logical frameworks to handle concepts in philosophy, computer science, and linguistics.
Core Principles of Classical Logic
Classical logic is founded on principles such as the law of excluded middle, which asserts that every proposition is either true or false, and the law of non-contradiction, which states that contradictory propositions cannot both be true simultaneously. It operates within a bivalent truth framework, where truth values are strictly binary, enabling definitive conclusions through formal proof systems like predicate and propositional calculus. Unlike modal logic, classical logic does not incorporate modalities such as necessity or possibility, focusing solely on absolute truth assessments.
Fundamental Concepts in Modal Logic
Modal logic extends classical logic by introducing modalities such as necessity (#) and possibility (*), which express statements about what must be true or what may be true, beyond mere truth values. Fundamental concepts in modal logic include possible worlds semantics, where truth is evaluated across various abstract scenarios or worlds, and accessibility relations that define connections between these worlds. Unlike classical logic's binary true/false evaluation, modal logic captures nuanced modes of truth, enabling formal reasoning about knowledge, belief, obligation, and time.
Syntax and Semantics: Comparing Structures
Modal logic extends classical logic by incorporating modal operators such as # (necessity) and * (possibility), enriching the syntax with formulas that express modality beyond truth-functional connectives. Its semantics utilize Kripke frames consisting of possible worlds and accessibility relations, enabling evaluation of formula truth relative to specific worlds, unlike classical logic, which relies solely on fixed truth valuations across propositions. This structural difference allows modal logic to capture notions of necessity, possibility, and contingency that classical logic's rigid truth tables cannot represent.
Expressive Power and Limitations
Modal logic extends classical logic by incorporating modalities such as necessity and possibility, enabling reasoning about concepts like knowledge, belief, and temporal events that classical logic cannot adequately express. While classical logic is limited to absolutes of truth and falsehood, modal logic's expressive power allows nuanced statements about possible worlds and hypothetical scenarios, enhancing its applicability in fields like computer science and philosophy. However, this increased expressiveness introduces complexity in model theory and proof systems, often making modal logic less decidable and harder to automate compared to classical logic.
Necessity and Possibility: Modal Operators Explained
Modal logic extends classical logic by introducing modal operators that express concepts of necessity (#) and possibility (*), allowing for nuanced truth evaluations beyond mere truth and falsehood. The necessity operator (#) asserts that a proposition must be true in all possible worlds, while the possibility operator (*) indicates that a proposition is true in at least one possible world. These modal operators enable reasoning about conditions like obligation, knowledge, and temporal states, which classical logic's binary framework cannot adequately capture.
Applications of Modal Logic
Modal logic extends classical logic by introducing necessity and possibility operators, enabling reasoning about knowledge, belief, time, and obligation. It is widely applied in computer science for verifying software and hardware systems, formalizing natural language semantics, and developing artificial intelligence protocols. Modal logic's ability to handle uncertainty and multiple truth values makes it essential in areas like epistemology, deontic reasoning, and dynamic system analysis.
Applications of Classical Logic
Classical logic, foundational in mathematics and computer science, underpins algorithms, automated theorem proving, and formal verification of software and hardware systems. Its binary truth values and well-defined inference rules enable precise problem solving, database querying, and artificial intelligence reasoning. Unlike modal logic, classical logic is widely applied in areas requiring definitive truth assessments without modality-based nuances.
Key Differences Between Modal and Classical Logic
Modal logic incorporates modalities such as necessity and possibility, extending classical logic's true or false framework by evaluating statements across possible worlds. Classical logic operates under bivalent truth values--true or false--without accounting for modal concepts, leading to more rigid deductive structures. The semantics of modal logic involve accessibility relations between possible worlds, enabling nuanced expressions of knowledge, belief, and obligation absent in classical logic.
Conclusion: Choosing the Right Logic Framework
Choosing the right logic framework depends on the nature of the problem: classical logic excels in deterministic scenarios with clear true/false values, while modal logic effectively handles concepts of necessity, possibility, and temporal dimensions. Modal logic's ability to express nuances like belief, knowledge, and obligation makes it essential for fields such as computer science, philosophy, and linguistics. Classical logic remains foundational for straightforward deductive reasoning and mathematical proofs, ensuring precise and unambiguous conclusions.
Modal logic Infographic
 libterm.com
libterm.com