Disjunctive reasoning allows conclusions to be drawn from two or more alternatives, where at least one must be true, such as in logical statements like "either A or B." This concept is vital in fields like mathematics, computer science, and philosophy, enabling clear decision-making despite uncertainty. Explore the rest of the article to deepen your understanding of disjunctive logic and its practical applications.
Table of Comparison
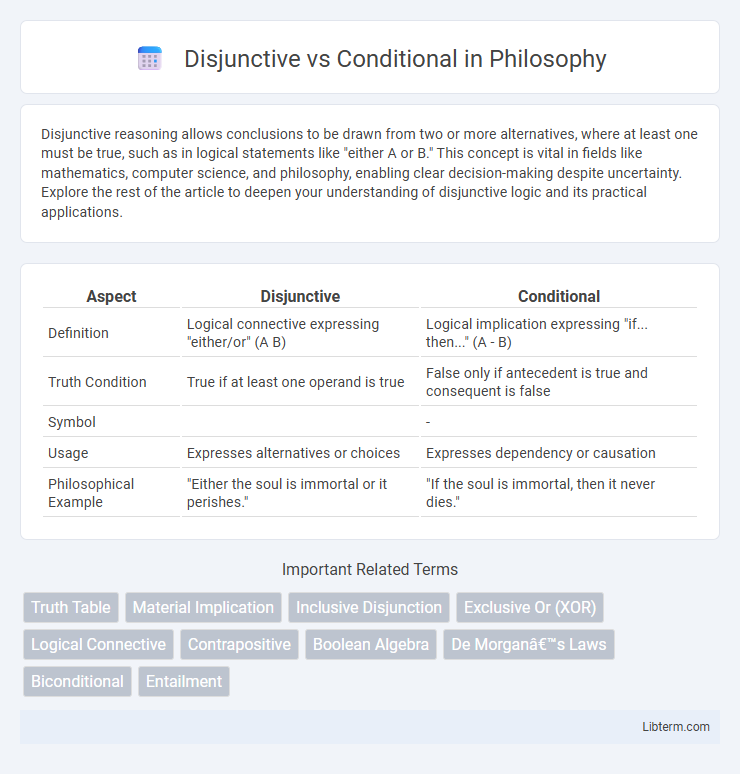
| Aspect | Disjunctive | Conditional |
|---|---|---|
| Definition | Logical connective expressing "either/or" (A B) | Logical implication expressing "if... then..." (A - B) |
| Truth Condition | True if at least one operand is true | False only if antecedent is true and consequent is false |
| Symbol | - | |
| Usage | Expresses alternatives or choices | Expresses dependency or causation |
| Philosophical Example | "Either the soul is immortal or it perishes." | "If the soul is immortal, then it never dies." |
Introduction to Disjunctive and Conditional Statements
Disjunctive statements use "or" to connect two or more conditions, indicating that at least one of them must be true for the overall statement to hold. Conditional statements follow an "if-then" structure, expressing that the truth of one proposition guarantees the truth of another. Understanding the logical relationships and truth values of disjunctive versus conditional statements is essential in formal logic and mathematical reasoning.
Definition of Disjunctive Statements
Disjunctive statements are logical expressions composed of two or more propositions joined by the logical operator "or," symbolized as , indicating that at least one of the propositions must be true for the entire statement to be true. In contrast, conditional statements use the "if-then" structure, represented as -, where the truth of one proposition (the antecedent) guarantees the truth of another (the consequent). Understanding the definition of disjunctive statements is essential in logic, computer science, and mathematics for constructing and evaluating compound logical expressions involving alternatives.
Definition of Conditional Statements
Conditional statements express a logical relationship where a specific outcome depends on the truth of a given condition, typically structured as "If P, then Q." These statements establish antecedent and consequent elements, indicating that Q follows from P only when P is true. Understanding conditionals is crucial in logic, programming, and mathematics for constructing arguments, algorithms, and proofs based on cause-and-effect relationships.
Key Differences Between Disjunctive and Conditional Logic
Disjunctive logic involves the use of "or" statements, where at least one of the propositions must be true, whereas conditional logic employs "if-then" statements, indicating that the truth of one proposition depends on the truth of another. In disjunctive logic, the truth value is true if any component is true, while in conditional logic, the statement is false only if the antecedent is true and the consequent is false. The key difference lies in their semantic structure: disjunctive logic represents alternatives, and conditional logic expresses dependency and implication.
Symbolic Representation in Logic
Disjunctive statements are symbolized using the logical operator , representing "or," as in \(P \vee Q\), indicating that at least one of the propositions \(P\) or \(Q\) is true. Conditional statements use the symbol - to denote "if-then" relationships, with \(P \rightarrow Q\) meaning if \(P\) is true, then \(Q\) must be true. The distinction in symbolic representation captures the difference between the inclusive alternative of disjunction and the directional implication of conditionals in formal logic.
Truth Tables for Disjunctive vs Conditional Statements
Disjunctive and conditional statements differ significantly in their truth tables: a disjunction (A B) is true if at least one component is true, while a conditional (A - B) is false only when the antecedent is true and the consequent is false. In the disjunctive truth table, the only false case occurs when both A and B are false, whereas the conditional truth table shows false exclusively when A is true and B is false. Understanding these distinctions is essential for applying logical reasoning in fields such as mathematics, computer science, and philosophy.
Common Uses in Reasoning and Argumentation
Disjunctive reasoning commonly employs "or" statements to explore alternative possibilities or choices, often used in decision-making scenarios to identify mutually exclusive outcomes. Conditional reasoning relies on "if-then" statements to establish cause-and-effect relationships or dependencies, playing a critical role in hypothesis testing and deductive arguments. Both approaches are fundamental in logical analysis, with disjunctive statements highlighting options and conditional statements emphasizing consequence and implication within structured arguments.
Examples Illustrating Each Statement Type
Disjunctive statements present alternatives like "You can have tea or coffee," emphasizing mutually exclusive options. Conditional statements, such as "If it rains, we will cancel the picnic," express a dependent relationship between two events. Understanding these examples clarifies how disjunctions offer choices while conditionals establish cause-and-effect scenarios.
Common Mistakes and Misconceptions
Disjunctive and conditional statements are often confused, leading to common mistakes such as interpreting "or" (disjunction) as implying a causal relationship like "if...then" (conditional). Misconceptions include believing that a conditional statement is true whenever the antecedent is false, whereas the truth of disjunction requires at least one true component. Clear distinction between inclusive and exclusive "or" prevents misinterpretation in logical reasoning and programming contexts.
Conclusion: Choosing the Right Statement Type
Choosing between disjunctive and conditional statements hinges on the logical relationship you want to express: disjunctive statements present alternatives with "or," while conditional statements establish cause-and-effect with "if-then." Disjunctive logic is ideal for scenarios requiring options or possibilities, whereas conditional logic suits contexts demanding dependency or implication between statements. For precise argumentation, align the statement type with the intended semantic function to enhance clarity and analytical rigor.
Disjunctive Infographic
 libterm.com
libterm.com