Entailment occurs when the truth of one statement logically guarantees the truth of another, reflecting a fundamental relationship in semantics and logic. Understanding entailment helps you analyze arguments, improve reasoning skills, and enhance natural language processing applications. Dive into the rest of the article to explore how entailment shapes communication and meaning.
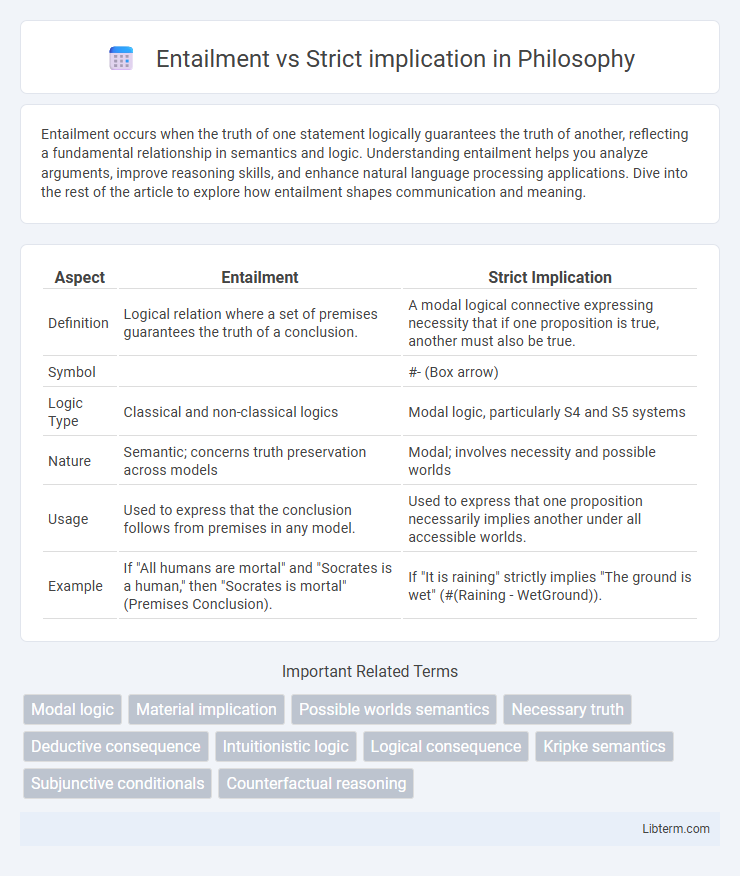
Table of Comparison
| Aspect | Entailment | Strict Implication |
|---|---|---|
| Definition | Logical relation where a set of premises guarantees the truth of a conclusion. | A modal logical connective expressing necessity that if one proposition is true, another must also be true. |
| Symbol | #- (Box arrow) | |
| Logic Type | Classical and non-classical logics | Modal logic, particularly S4 and S5 systems |
| Nature | Semantic; concerns truth preservation across models | Modal; involves necessity and possible worlds |
| Usage | Used to express that the conclusion follows from premises in any model. | Used to express that one proposition necessarily implies another under all accessible worlds. |
| Example | If "All humans are mortal" and "Socrates is a human," then "Socrates is mortal" (Premises Conclusion). | If "It is raining" strictly implies "The ground is wet" (#(Raining - WetGround)). |
Understanding Entailment: A Semantic Perspective
Entailment in semantics refers to a relationship where the truth of one statement guarantees the truth of another within a given interpretation, emphasizing necessity across all models that satisfy the premise. Unlike strict implication, which operates within modal logic involving necessity operators, entailment is purely about the preservation of truth in all possible scenarios consistent with the premise. Understanding entailment requires analyzing logical consequence through model theory, ensuring that if the set of premises is true, the conclusion must also be true without exception.
Defining Strict Implication in Logic
Strict implication in logic is a modal relationship that asserts necessity between propositions, meaning if the antecedent is true, the consequent must be true in all possible worlds. Unlike entailment, which is a broader semantic relation indicating truth preservation from premises to conclusion, strict implication requires the implication to hold necessarily, not just truthfully. This concept plays a crucial role in modal logic by formalizing the idea of implication beyond classical truth-functional logic, emphasizing the modal necessity of the consequent given the antecedent.
Core Differences Between Entailment and Strict Implication
Entailment is a semantic relation where a set of premises guarantees the truth of a conclusion in every possible interpretation, ensuring logical consequence across all models. Strict implication, rooted in modal logic, requires that if the antecedent is true in every accessible world, then the consequent must also be true in those worlds, reflecting necessity rather than mere truth preservation. The core difference lies in entailment's focus on truth preservation across all models, while strict implication emphasizes necessity within modal frameworks and possible world semantics.
Philosophical Foundations of Entailment
Entailment, rooted in the principles of logical consequence, asserts that if the premises are true, the conclusion must necessarily be true, reflecting a fundamental relation in classical logic and semantic theory. Strict implication, a modal logic concept introduced by C.I. Lewis, strengthens material implication by requiring the necessity of the connection between antecedent and consequent across all possible worlds. The philosophical foundations of entailment emphasize truth-preserving inference essential for sound reasoning, whereas strict implication captures a modal necessity that underscores the epistemic or metaphysical dependence in conditional statements.
Modal Logic and the Concept of Strict Implication
In modal logic, entailment refers to a semantic relationship where a set of premises necessarily leads to a conclusion in every possible world, ensuring truth preservation across models. Strict implication, introduced by C.I. Lewis, enhances classical material implication by requiring that if the antecedent is necessarily true, then the consequent must also be necessarily true, thereby embedding necessity into the implication itself. This distinction emphasizes that strict implication is a modal operator capturing a stronger, necessity-based form of logical consequence beyond mere truth-functional entailment.
Truth Preservation in Entailment vs Strict Implication
Entailment ensures truth preservation from premises to conclusion across all models where the premises are true, meaning if the premises are true, the conclusion must also be true. Strict implication, defined within modal logic, requires that the implication is necessarily true in all possible worlds, emphasizing necessity rather than just the preservation of truth in actual scenarios. This distinction shows entailment as a semantic relation focused on truth conditions, while strict implication adds a modal necessity layer to truth preservation.
Applications in Mathematics and Formal Reasoning
Entailment in mathematics ensures truth preservation across all models, vital for validating logical arguments and proofs within formal systems like predicate logic. Strict implication strengthens this by requiring necessity in modal logic frameworks, supporting applications in modal proof theory and automated reasoning tools. Both concepts underpin the development of formal verification methods and enhance automated theorem proving by distinguishing between semantic consequence and modal necessity.
Common Misconceptions and Clarifications
Entailment in logic means that if a set of premises is true, the conclusion must also be true in every model, whereas strict implication involves necessity across all possible worlds, often within modal logic frameworks. A common misconception is treating strict implication as merely a stronger form of material implication, but it actually requires a modal interpretation that material implication lacks. Clarifying this distinction helps avoid errors in logical reasoning and ensures precise communication in formal semantics and philosophical logic.
Practical Examples Illustrating Key Differences
Entailment in logic means that if the premises are true, the conclusion must also be true, such as "All humans are mortal" entails "Socrates is mortal" when "Socrates is a human" is given. Strict implication involves necessity within modal logic, where "If p strictly implies q," then in all possible worlds where p is true, q must also be true, exemplified by "If it is raining necessarily, then the ground is necessarily wet." The key difference lies in entailment's focus on truth preservation in actual situations, whereas strict implication emphasizes modal necessity across all possible worlds.
Impacts on Logical Systems and Computation
Entailment ensures that whenever a set of premises is true, the conclusion must also be true, providing a foundation for sound logical inference in formal systems. Strict implication, interpreted as necessity within modal logic, strengthens the relationship by requiring that the implication holds in all possible worlds, impacting computational complexity by influencing decision procedures and proof systems. This distinction affects the design of automated theorem proving and logic programming by determining the robustness and expressiveness of inference mechanisms.
Entailment Infographic
 libterm.com
libterm.com