Fuzzy logic enhances decision-making by handling uncertainty and imprecision, mimicking human reasoning more closely than traditional binary systems. It is widely applied in control systems, artificial intelligence, and data analysis to improve accuracy and flexibility. Discover how your technology or business can benefit from integrating fuzzy logic by reading the full article.
Table of Comparison
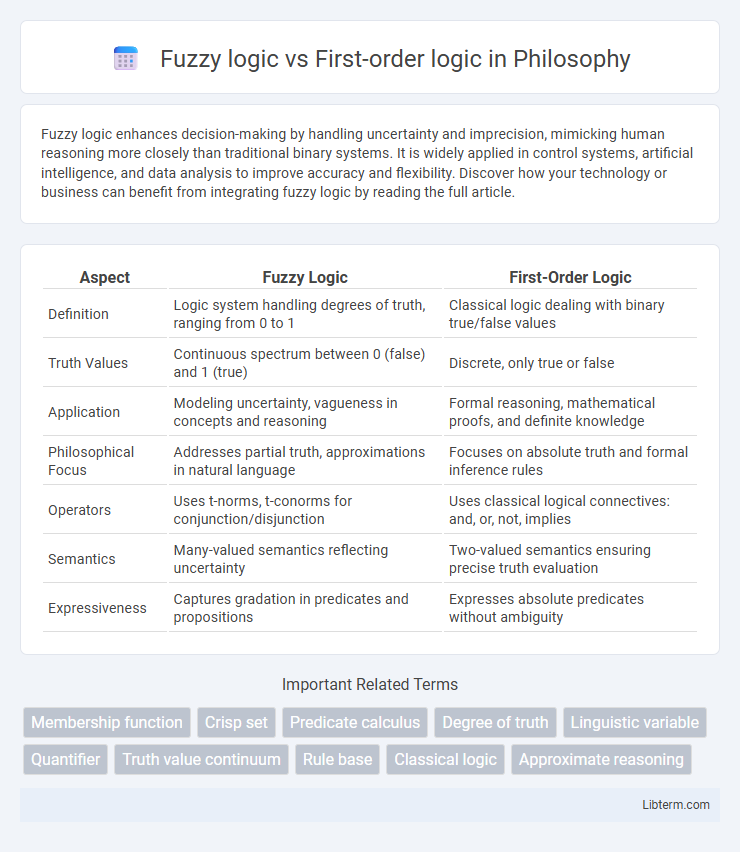
| Aspect | Fuzzy Logic | First-Order Logic |
|---|---|---|
| Definition | Logic system handling degrees of truth, ranging from 0 to 1 | Classical logic dealing with binary true/false values |
| Truth Values | Continuous spectrum between 0 (false) and 1 (true) | Discrete, only true or false |
| Application | Modeling uncertainty, vagueness in concepts and reasoning | Formal reasoning, mathematical proofs, and definite knowledge |
| Philosophical Focus | Addresses partial truth, approximations in natural language | Focuses on absolute truth and formal inference rules |
| Operators | Uses t-norms, t-conorms for conjunction/disjunction | Uses classical logical connectives: and, or, not, implies |
| Semantics | Many-valued semantics reflecting uncertainty | Two-valued semantics ensuring precise truth evaluation |
| Expressiveness | Captures gradation in predicates and propositions | Expresses absolute predicates without ambiguity |
Introduction to Fuzzy Logic and First-Order Logic
Fuzzy logic extends classical logic by handling reasoning that is approximate rather than fixed and exact, representing truth values between completely true and completely false to model uncertainty and vagueness. First-order logic, also known as predicate logic, focuses on quantifying variables and defining relations with true or false values, enabling precise expression of structured knowledge using predicates, quantifiers, and logical connectives. While first-order logic relies on binary truth values, fuzzy logic introduces degrees of truth, making it suitable for real-world scenarios involving imprecise or incomplete information.
Core Principles of Fuzzy Logic
Fuzzy logic operates on the principle of partial truth values between 0 and 1, enabling it to handle uncertainty and vagueness in data, unlike first-order logic which relies on binary true or false values. Core principles of fuzzy logic include fuzzy set theory, where membership functions define the degree of belonging, and approximate reasoning, facilitating inference in imprecise environments. This approach allows for more flexible and human-like reasoning in complex systems such as control and decision-making applications.
Fundamentals of First-Order Logic
First-order logic (FOL) is a formal system used in mathematics, philosophy, and computer science that extends propositional logic by incorporating quantified variables over non-logical objects. It utilizes predicates, quantifiers such as "forall" () and "exists" (), and allows expressions about properties and relations of objects within a domain. Unlike fuzzy logic, which handles degrees of truth, first-order logic operates under binary truth values, enabling precise reasoning through well-defined syntax and semantics.
Key Differences Between Fuzzy Logic and First-Order Logic
Fuzzy logic handles reasoning with degrees of truth, representing uncertainty through values between 0 and 1, while first-order logic relies on binary true or false values for precise and deterministic reasoning. Fuzzy logic is effective for modeling imprecise concepts and approximate reasoning in real-world scenarios, whereas first-order logic excels in formalizing relationships and quantifying over objects with strict logical rules. The key difference lies in fuzziness allowing partial truth, contrasting with first-order logic's definitive true/false semantics and quantifiers like (for all) and (there exists).
Applications of Fuzzy Logic
Fuzzy logic excels in applications requiring reasoning with uncertain or imprecise information, such as control systems in household appliances, automotive systems, and decision-making in medical diagnosis. It models linguistic variables and handles partial truth values between 0 and 1, enabling flexible control and adaptive learning in robotics and artificial intelligence. Unlike first-order logic, which deals with binary true/false evaluations, fuzzy logic provides a more nuanced approach to reasoning in complex real-world scenarios.
Applications of First-Order Logic
First-order logic is extensively used in artificial intelligence for knowledge representation, allowing systems to model complex relationships and reason about objects and their properties. In formal verification, it provides a rigorous framework to prove the correctness of algorithms and hardware designs through theorem proving techniques. Additionally, first-order logic underpins natural language processing by enabling the formal analysis of sentence structures and semantic interpretations.
Strengths of Fuzzy Logic
Fuzzy logic excels in handling uncertainty and imprecision by allowing variables to have degrees of truth rather than binary true/false values, making it ideal for real-world applications where data is often vague or incomplete. It enables more human-like reasoning and decision-making processes in systems such as control mechanisms, expert systems, and natural language processing. Unlike first-order logic, which requires crisp and well-defined predicates, fuzzy logic adapts seamlessly to nonlinear and complex environments, improving flexibility and robustness in problem-solving.
Strengths of First-Order Logic
First-order logic excels in expressiveness and precision, enabling the representation of complex relationships and quantification over individuals, which supports rigorous mathematical reasoning and formal proofs. Its well-defined syntax and semantics allow for automated theorem proving and consistency checking, making it indispensable in fields like artificial intelligence, knowledge representation, and formal verification. Unlike fuzzy logic, first-order logic operates with binary truth values, providing clarity and unambiguous conclusions essential for applications requiring strict logical inference.
Limitations and Challenges
Fuzzy logic, while effective for handling uncertainty and imprecision in real-world scenarios, faces challenges such as interpretability issues and difficulty in expressing complex relational structures compared to First-order logic. First-order logic excels in formal reasoning with well-defined semantics but struggles with representing uncertain or vague information and computational inefficiency in large-scale problems. Both frameworks encounter limitations in scalability and reasoning complexity when applied to dynamic, real-world applications requiring nuanced decision-making.
Choosing the Right Logic System for Your Needs
Fuzzy logic handles uncertainty and partial truth values, making it ideal for applications requiring approximate reasoning and real-world ambiguity, such as control systems and decision-making under imprecision. First-order logic excels in scenarios demanding rigorous, exact inference with well-defined, binary true/false conditions, commonly used in formal verification and knowledge representation. Selecting the right logic system depends on the nature of the problem: prioritize fuzzy logic for nuanced, graded truth evaluation and first-order logic for precise, deterministic reasoning tasks.
Fuzzy logic Infographic
 libterm.com
libterm.com