Constructivism emphasizes that knowledge is actively built by learners through experience and reflection rather than passively received. This educational theory highlights the importance of context and social interaction in developing understanding. Explore the rest of the article to see how constructivism can transform your approach to learning and teaching.
Table of Comparison
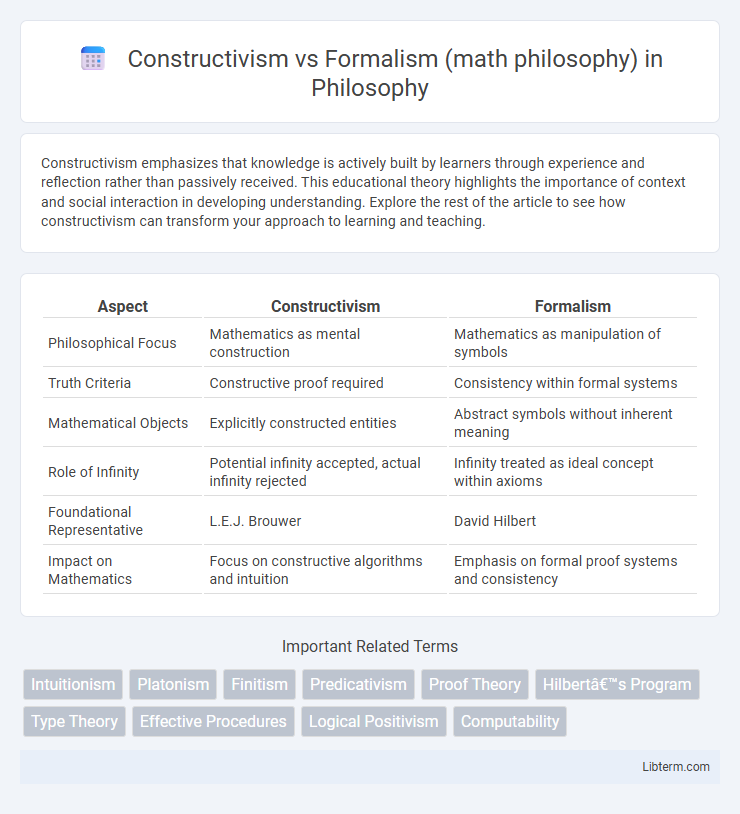
| Aspect | Constructivism | Formalism |
|---|---|---|
| Philosophical Focus | Mathematics as mental construction | Mathematics as manipulation of symbols |
| Truth Criteria | Constructive proof required | Consistency within formal systems |
| Mathematical Objects | Explicitly constructed entities | Abstract symbols without inherent meaning |
| Role of Infinity | Potential infinity accepted, actual infinity rejected | Infinity treated as ideal concept within axioms |
| Foundational Representative | L.E.J. Brouwer | David Hilbert |
| Impact on Mathematics | Focus on constructive algorithms and intuition | Emphasis on formal proof systems and consistency |
Introduction to Constructivism and Formalism
Constructivism in mathematics emphasizes the necessity of constructing mathematical objects explicitly and views existence as tied to our ability to construct these objects, rejecting non-constructive proofs common in classical mathematics. Formalism, pioneered by David Hilbert, treats mathematics as a manipulation of symbols within a formal system governed by axioms and rules, focusing on consistency and completeness rather than ontological existence. Both philosophies address the foundations of mathematics but differ fundamentally in their interpretation of mathematical truth--constructivism demands constructive proof, while formalism prioritizes syntactic derivations within formal frameworks.
Historical Context and Development
Constructivism in mathematics originated in the early 20th century as a response to the foundational crises initiated by paradoxes in naive set theory, emphasizing explicit construction of mathematical objects. Formalism, championed by David Hilbert, sought to establish mathematics on a consistent, complete system of formal symbols and rules without necessarily assigning intrinsic meaning. The historical development of these philosophies reflects a fundamental debate between constructively verifiable truth and symbolic manipulation, shaping the evolution of modern mathematical logic and proof theory.
Core Principles of Constructivism
Constructivism in mathematics emphasizes that mathematical objects must be explicitly constructed and that existence proofs require a constructive method, rejecting non-constructive proofs allowed in Formalism. Core principles include the insistence on algorithmic procedures and the avoidance of the law of excluded middle, ensuring all mathematical statements have constructive validity. This philosophy contrasts with Formalism's focus on manipulating symbols according to formal rules without requiring constructive evidence.
Fundamental Tenets of Formalism
Formalism in the philosophy of mathematics asserts that mathematics is a manipulation of symbols according to specified rules without inherent meaning. Central tenets include the view that mathematical statements are formal expressions, and mathematical proof involves derivations within axiomatic systems. This perspective emphasizes consistency, completeness, and syntactic structure over semantic interpretation or constructive existence of mathematical objects.
Key Differences: Constructivist vs. Formalist Approaches
Constructivism in mathematics emphasizes the necessity of explicit constructions and constructive proofs, rejecting non-constructive existence proofs and relying on intuitionistic logic. Formalism treats mathematics as a manipulation of symbols based on formal axioms without requiring constructive evidence, accepting classical logic and non-constructive methods. The key difference lies in constructivism's insistence on mathematical objects' constructive existence versus formalism's focus on formal consistency and derivability within axiomatic systems.
Impact on Mathematical Proof and Truth
Constructivism demands that mathematical proofs provide explicit constructions and verifiable algorithms, rejecting non-constructive existence proofs common in Formalism. Formalism emphasizes consistency of axiomatic systems and treats proofs as symbol manipulations within formal languages, prioritizing syntactic rigor over semantic content. This philosophical divergence impacts the notion of mathematical truth: Constructivism ties truth to constructive provability, while Formalism regards truth as derivable from formal systems regardless of constructive content.
Notable Figures in Constructivism and Formalism
Notable figures in Constructivism include L.E.J. Brouwer, who pioneered intuitionism emphasizing mathematics as a mental construction, and Errett Bishop, known for developing constructive analysis. Formalism is chiefly associated with David Hilbert, who sought to formalize all mathematics through axiomatic systems and proof theory, and Paul Bernays, who contributed significantly to Hilbert's program. These mathematicians shaped distinct philosophies: Constructivists prioritize constructive proofs and algorithms, while Formalists focus on abstract axiomatic frameworks and consistency.
Influence on Modern Mathematics
Constructivism emphasizes mathematical objects' explicit construction, influencing algorithm development and proof techniques in computer science and constructive analysis. Formalism prioritizes symbolic manipulation within formal systems, shaping foundational studies and automated theorem proving. Both philosophies significantly impact modern mathematics by guiding research directions and foundational frameworks in logic, computation, and mathematical rigor.
Philosophical Critiques and Debates
Constructivism challenges classical formalism by rejecting non-constructive proofs and emphasizing mathematical objects as explicitly constructed entities, which raises debates on the nature of mathematical existence. Formalism, advocating for mathematics as manipulation of symbols according to rules, faces critiques for ignoring semantic meaning and the philosophical grounding of mathematical truth. Philosophers argue that constructivism better captures mathematical intuition and epistemology, while formalism's abstraction can lead to questions about the ontological status of mathematical statements.
Conclusion: Synthesizing Perspectives
Constructivism and Formalism offer distinct yet complementary views on the foundations of mathematics, with Constructivism emphasizing explicit constructions and mathematical objects verified through computation, while Formalism prioritizes the manipulation of symbols within formal systems and axioms. Synthesizing these perspectives highlights the balance between rigorous proof frameworks and the constructive processes that ensure mathematical objects' existence. Recognizing this synergy enriches foundational studies by integrating computational validation with symbolic formalism, advancing both theoretical understanding and practical application.
Constructivism Infographic
 libterm.com
libterm.com