Fuzzy logic mimics human reasoning by handling uncertainty and partial truth, making it ideal for complex decision-making systems in AI, control systems, and data analysis. This approach extends classical binary logic by allowing values between true and false, enabling more nuanced and flexible problem-solving. Discover how understanding fuzzy logic can enhance your ability to design smarter, adaptive technologies by reading the full article.
Table of Comparison
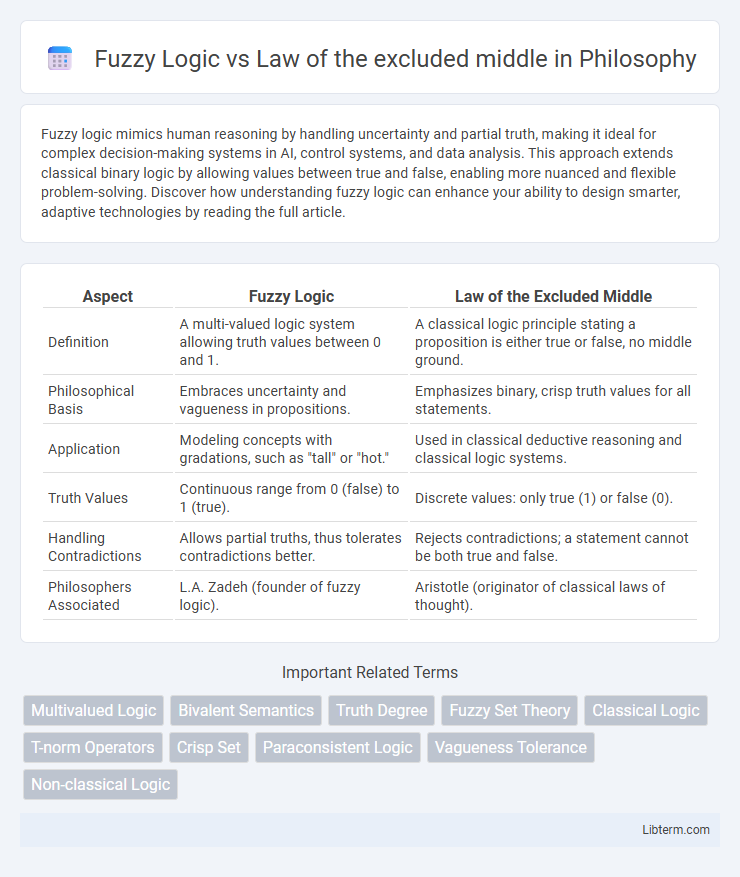
| Aspect | Fuzzy Logic | Law of the Excluded Middle |
|---|---|---|
| Definition | A multi-valued logic system allowing truth values between 0 and 1. | A classical logic principle stating a proposition is either true or false, no middle ground. |
| Philosophical Basis | Embraces uncertainty and vagueness in propositions. | Emphasizes binary, crisp truth values for all statements. |
| Application | Modeling concepts with gradations, such as "tall" or "hot." | Used in classical deductive reasoning and classical logic systems. |
| Truth Values | Continuous range from 0 (false) to 1 (true). | Discrete values: only true (1) or false (0). |
| Handling Contradictions | Allows partial truths, thus tolerates contradictions better. | Rejects contradictions; a statement cannot be both true and false. |
| Philosophers Associated | L.A. Zadeh (founder of fuzzy logic). | Aristotle (originator of classical laws of thought). |
Introduction to Fuzzy Logic and the Law of the Excluded Middle
Fuzzy Logic extends classical Boolean logic by allowing truth values to range continuously between 0 and 1, enabling reasoning with uncertainty and partial truth. The Law of the Excluded Middle is a principle in classical logic stating that every proposition is either true or false, with no middle ground, forming the foundation of traditional binary reasoning. Fuzzy Logic challenges this binary framework by modeling degrees of truth, which is essential in complex systems like control engineering, artificial intelligence, and decision-making processes.
Defining the Law of the Excluded Middle
The Law of the Excluded Middle is a fundamental principle in classical logic stating that any proposition must be either true or false, with no middle ground. Fuzzy logic challenges this binary constraint by allowing truth values to exist on a continuum between true and false, reflecting degrees of truth. This contrast highlights fuzzy logic's ability to model uncertainty and vagueness in real-world situations where the Law of the Excluded Middle is insufficient.
Fundamentals of Fuzzy Logic
Fuzzy logic challenges the Law of the Excluded Middle by allowing truth values to range continuously between 0 and 1, rather than restricting them to binary true or false states. This approach more closely models real-world uncertainty and vagueness by assigning degrees of membership to sets, enabling nuanced reasoning in complex systems. Core to fuzzy logic is the concept of fuzzy sets, where elements partially belong to multiple sets simultaneously, facilitating flexible decision-making and control in fields such as artificial intelligence and automated systems.
Key Differences between Fuzzy Logic and Classical Logic
Fuzzy logic allows for degrees of truth values ranging between 0 and 1, enabling the representation of partial truths, whereas classical logic strictly adheres to the Law of the Excluded Middle, where statements are either true or false with no intermediate values. Unlike classical binary logic, fuzzy logic handles uncertainty and vagueness by employing membership functions that quantify the extent to which an element belongs to a set. This fundamental difference makes fuzzy logic more suitable for modeling real-world phenomena with imprecise data, while classical logic applies to well-defined, dichotomous conditions.
Practical Applications of Fuzzy Logic
Fuzzy logic enables decision-making in complex, real-world systems by handling degrees of truth rather than rigid binaries, unlike the law of the excluded middle which enforces strict true-or-false conditions. Practical applications of fuzzy logic include control systems for household appliances like washing machines and air conditioners, where it adjusts operations based on imprecise inputs such as temperature or dirtiness levels. It also excels in fields like automotive systems for adaptive cruise control and artificial intelligence for natural language processing, offering flexible reasoning in uncertain environments.
Limitations of the Law of the Excluded Middle
The Law of the Excluded Middle, a principle in classical logic, asserts that every proposition is either true or false, excluding any intermediate truth values. This binary framework limits its applicability in real-world scenarios where uncertainty, vagueness, or partial truth are prevalent, such as in natural language processing and decision-making systems. Fuzzy Logic addresses this limitation by allowing truth values to range continuously between 0 and 1, enabling more nuanced reasoning in complex, ambiguous environments.
Fuzzy Sets vs. Binary Logic
Fuzzy logic introduces fuzzy sets that allow elements to have degrees of membership ranging between 0 and 1, challenging the binary logic foundation of the law of the excluded middle, which permits only true or false values. Unlike binary logic's rigid classification, fuzzy sets accommodate uncertainty and partial truth, enabling more nuanced and flexible reasoning in systems such as control engineering and decision-making. This fundamental difference makes fuzzy logic highly effective in modeling real-world scenarios where binary categorizations fail to capture complexity.
Real-World Examples Illustrating Both Concepts
Fuzzy logic models real-world scenarios like temperature control systems where values range between completely hot and cold, allowing for partial truths such as "somewhat warm," unlike the Law of the Excluded Middle which asserts that propositions must be either true or false without any middle ground. In legal contexts, the Law of the Excluded Middle dictates judgments must classify statements strictly as guilty or not guilty, whereas fuzzy logic enables nuanced interpretations in medical diagnoses where symptoms may partially indicate conditions rather than absolute presence or absence. Traffic light control systems exemplify fuzzy logic by adjusting signal durations based on traffic density gradients, contrasting binary traffic rules grounded in the Law of the Excluded Middle that enforce strict stop-or-go decisions.
Philosophical Implications and Debates
Fuzzy logic challenges the classical Law of the Excluded Middle by allowing truth values to exist on a continuum between true and false, prompting philosophical debates about the nature of truth and binary oppositions. This shift enables more nuanced reasoning in contexts where ambiguity and vagueness are inherent, reshaping foundational assumptions in epistemology and logic. Philosophers argue whether fuzzy logic offers a more accurate representation of real-world scenarios or undermines the rigor of classical logical principles.
Conclusion: Choosing Between Fuzzy Logic and the Law of the Excluded Middle
Choosing between Fuzzy Logic and the Law of the Excluded Middle depends on the nature of the problem and the required precision. Fuzzy Logic excels in handling uncertainty and partial truths in complex, real-world scenarios, while the Law of the Excluded Middle suits classical binary decisions where propositions are strictly true or false. The decision hinges on whether ambiguity and gradation are integral to the system or a clear-cut true/false distinction suffices.
Fuzzy Logic Infographic
 libterm.com
libterm.com