Fuzzy logic offers a flexible approach to reasoning, mimicking human decision-making by handling imprecise or uncertain information effectively. It enhances control systems, artificial intelligence, and expert systems by allowing values between true and false rather than binary states. Explore the rest of the article to discover how fuzzy logic can improve your problem-solving strategies.
Table of Comparison
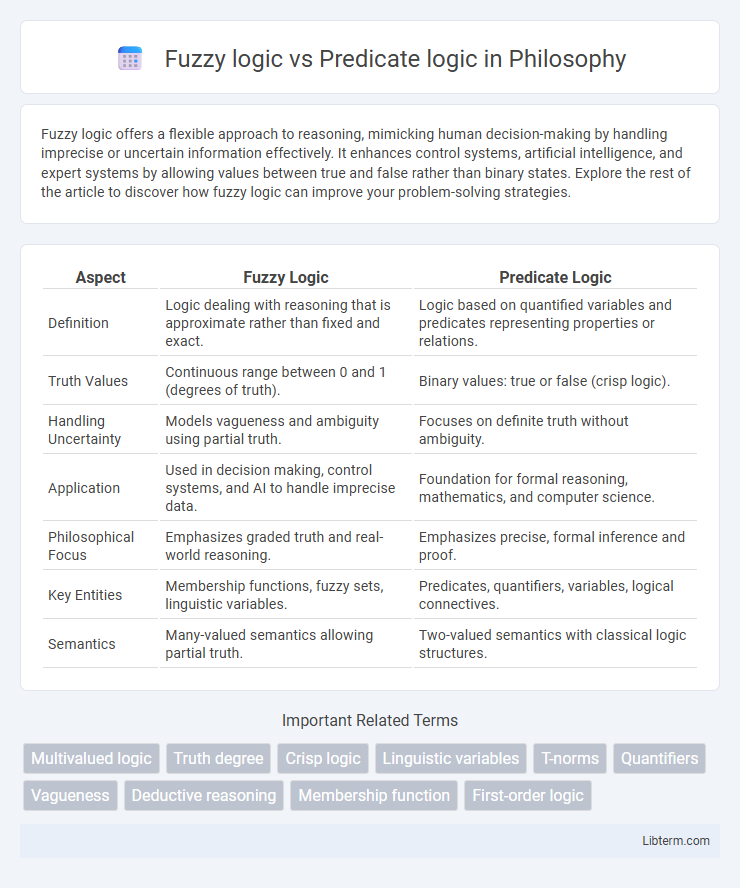
| Aspect | Fuzzy Logic | Predicate Logic |
|---|---|---|
| Definition | Logic dealing with reasoning that is approximate rather than fixed and exact. | Logic based on quantified variables and predicates representing properties or relations. |
| Truth Values | Continuous range between 0 and 1 (degrees of truth). | Binary values: true or false (crisp logic). |
| Handling Uncertainty | Models vagueness and ambiguity using partial truth. | Focuses on definite truth without ambiguity. |
| Application | Used in decision making, control systems, and AI to handle imprecise data. | Foundation for formal reasoning, mathematics, and computer science. |
| Philosophical Focus | Emphasizes graded truth and real-world reasoning. | Emphasizes precise, formal inference and proof. |
| Key Entities | Membership functions, fuzzy sets, linguistic variables. | Predicates, quantifiers, variables, logical connectives. |
| Semantics | Many-valued semantics allowing partial truth. | Two-valued semantics with classical logic structures. |
Introduction to Fuzzy Logic and Predicate Logic
Fuzzy logic extends classical predicate logic by handling partial truth values between 0 and 1, enabling reasoning with uncertain or imprecise information, whereas predicate logic relies on binary true or false values for precise statements. Predicate logic serves as the foundation of formal reasoning and mathematical proofs with clear, well-defined predicates and quantifiers, while fuzzy logic models vagueness found in real-world scenarios such as natural language processing and control systems. The key difference lies in fuzzy logic's ability to accommodate gradations of truth, making it suitable for applications requiring approximate reasoning beyond the rigid structure of traditional predicate logic.
Historical Background and Evolution
Fuzzy logic originated in the 1960s through Lotfi Zadeh's work to address reasoning with uncertainty and partial truth, evolving from classical binary logic to accommodate degrees of truth. Predicate logic, developed in the early 20th century by Gottlob Frege and further formalized by Bertrand Russell and Alfred North Whitehead, established a foundation for symbolic reasoning through quantifiers and predicates in formal systems. Over time, fuzzy logic expanded into control systems and artificial intelligence, while predicate logic became a cornerstone of mathematical logic and computer science for theorem proving and formal verification.
Fundamental Concepts and Definitions
Fuzzy logic introduces the concept of partial truth values between 0 and 1, allowing reasoning with uncertainty and vagueness, whereas predicate logic relies on crisp, binary truth values of true or false. Predicate logic uses quantifiers and predicates to express relationships and properties in a domain, operating under classical Boolean semantics. Fuzzy logic extends classical logic by defining membership functions for fuzzy sets, enabling more flexible and approximate reasoning in complex systems.
Differences in Logical Reasoning
Fuzzy logic handles reasoning with degrees of truth, allowing variables to have truth values between 0 and 1, which models uncertainty and imprecision effectively. Predicate logic relies on binary true or false values, providing precise and exact logical deductions based on well-defined predicates and quantifiers. The fundamental difference lies in fuzzy logic's ability to reason about partial truths, whereas predicate logic requires strict dichotomous truth conditions for valid inference.
Mathematical Formalism Comparison
Fuzzy logic utilizes degrees of truth represented by values between 0 and 1, allowing partial membership through membership functions, while predicate logic operates on binary truth values (true or false) using quantifiers and predicates defined over domains. Mathematically, fuzzy logic extends classical set theory with fuzzy sets characterized by membership functions m: X - [0,1], contrasting with predicate logic's crisp sets and Boolean algebra. Predicate logic formalism is based on first-order logic syntax and semantics with precise truth assignments, whereas fuzzy logic incorporates lattice theory and fuzzy inference systems to handle uncertainty and vagueness mathematically.
Handling Uncertainty and Vagueness
Fuzzy logic excels in handling uncertainty and vagueness by allowing partial membership in sets using degrees of truth between 0 and 1, enabling more flexible and human-like reasoning in imprecise environments. Predicate logic, in contrast, relies on binary true or false values and precise predicates, making it less effective for modeling real-world scenarios with ambiguous or incomplete information. This fundamental difference makes fuzzy logic particularly advantageous in fields like control systems and decision-making where uncertainty is inherent.
Applications in Real-world Scenarios
Fuzzy logic excels in real-world scenarios requiring handling of uncertainty and imprecision, such as climate control systems, medical diagnosis, and consumer electronics, by enabling approximate reasoning with degrees of truth. Predicate logic, with its foundation in formal reasoning and binary truth values, is predominant in knowledge representation, automated theorem proving, and database query languages where precise, well-defined relationships are essential. Both logics serve critical roles: fuzzy logic models complex, ambiguous data, while predicate logic underpins rigorous inference and symbolic computation in AI and formal verification.
Strengths and Limitations
Fuzzy logic excels in handling uncertainty and imprecision by allowing partial truth values between 0 and 1, making it ideal for real-world scenarios with vague or ambiguous data, but it lacks the formal rigor and expressiveness of predicate logic. Predicate logic offers precise, well-defined structures and is powerful for reasoning about relationships and quantifiers in complex systems, yet it struggles with ambiguity and incomplete information. The strengths of fuzzy logic lie in approximate reasoning and adaptability, while predicate logic is strong in formal proof, consistency, and detailed logical inference, highlighting their complementary roles in artificial intelligence and computational logic.
Integration and Hybrid Approaches
Integration of fuzzy logic and predicate logic enables systems to handle both uncertainty and strict logical reasoning, enhancing decision-making in complex environments. Hybrid approaches combine fuzzy sets with first-order logic to represent imprecise information alongside structured knowledge, improving inference accuracy in AI applications. Techniques such as fuzzy predicate logic extend classical frameworks, supporting reasoning under vagueness while maintaining formal logic properties for robust computational models.
Future Trends and Research Directions
Future trends in fuzzy logic emphasize its integration with machine learning and big data analytics to handle uncertainty and imprecision in real-world applications more effectively. Predicate logic research focuses on improving automated theorem proving and formal verification techniques with advancements in quantum computing and explainable AI. Emerging hybrid systems combining fuzzy logic's tolerance for ambiguity and predicate logic's precise reasoning are poised to enable more robust and adaptable intelligent systems.
Fuzzy logic Infographic
 libterm.com
libterm.com