Syllogistic logic is a fundamental form of deductive reasoning that uses categorical propositions to derive conclusions from two premises. It helps analyze arguments by breaking them down into standard forms involving subjects and predicates, enabling clear assessment of validity. Explore the rest of the article to enhance your understanding of how syllogistic logic sharpens critical thinking skills.
Table of Comparison
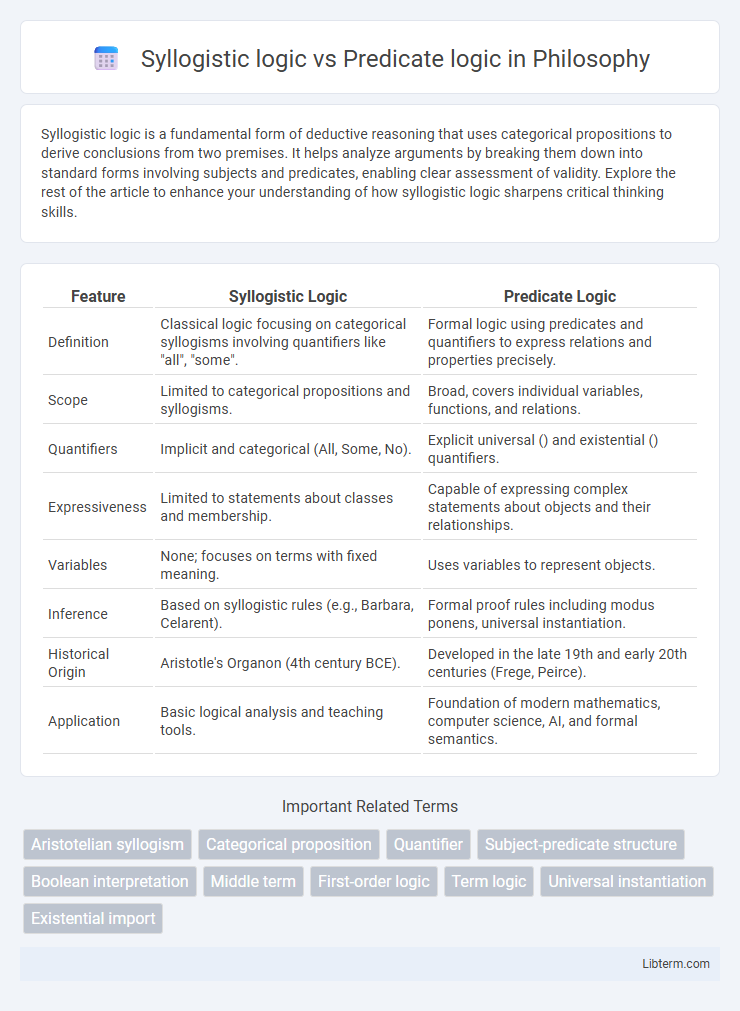
| Feature | Syllogistic Logic | Predicate Logic |
|---|---|---|
| Definition | Classical logic focusing on categorical syllogisms involving quantifiers like "all", "some". | Formal logic using predicates and quantifiers to express relations and properties precisely. |
| Scope | Limited to categorical propositions and syllogisms. | Broad, covers individual variables, functions, and relations. |
| Quantifiers | Implicit and categorical (All, Some, No). | Explicit universal () and existential () quantifiers. |
| Expressiveness | Limited to statements about classes and membership. | Capable of expressing complex statements about objects and their relationships. |
| Variables | None; focuses on terms with fixed meaning. | Uses variables to represent objects. |
| Inference | Based on syllogistic rules (e.g., Barbara, Celarent). | Formal proof rules including modus ponens, universal instantiation. |
| Historical Origin | Aristotle's Organon (4th century BCE). | Developed in the late 19th and early 20th centuries (Frege, Peirce). |
| Application | Basic logical analysis and teaching tools. | Foundation of modern mathematics, computer science, AI, and formal semantics. |
Introduction to Syllogistic and Predicate Logic
Syllogistic logic, developed by Aristotle, focuses on categorical syllogisms involving quantifiers like "all," "some," and "none" to deduce conclusions from two premises. Predicate logic extends syllogistic logic by introducing predicates and quantified variables, enabling more precise representation of statements and relationships within domains. Unlike syllogistic logic's limitation to subject-predicate structures, predicate logic supports complex expressions using functions, predicates, and logical connectives, making it foundational for formal semantics and mathematical logic.
Historical Background of Syllogistic Logic
Syllogistic logic, developed by Aristotle in the 4th century BCE, represents one of the earliest formal systems of deductive reasoning based on categorical propositions. This classical logical framework centers on syllogisms, which are arguments consisting of two premises and a conclusion, each involving quantified terms like "all," "some," or "none." Unlike predicate logic, which emerged in the late 19th century with Gottlob Frege to handle relationships and quantification more precisely, syllogistic logic laid the foundational principles of formal logic influencing medieval scholasticism and early modern philosophy.
Foundations of Predicate Logic
Syllogistic logic, developed by Aristotle, centers on categorical syllogisms involving terms and their relationships, limiting its expressive power to a fixed set of forms. Predicate logic extends beyond this by introducing quantifiers and variables, enabling the representation of more complex statements involving properties and relations of objects. The foundations of predicate logic lie in its formal syntax and semantics, which provide a rigorous framework for modeling inference in mathematics, computer science, and linguistics.
Key Differences Between Syllogistic and Predicate Logic
Syllogistic logic primarily deals with categorical propositions involving quantifiers like "all," "some," or "none" in a fixed subject-predicate structure, while predicate logic extends this by incorporating variables, functions, and relations to express more complex statements. Predicate logic allows for multiple quantifiers and nested expressions, enabling a richer and more precise representation of logical relationships than the limited two-term format of syllogistic logic. The formal syntax and semantics of predicate logic provide a foundation for modern logic and computational reasoning, making it more versatile than the traditional, more rigid syllogistic framework.
Structure and Syntax: Syllogisms vs Predicates
Syllogistic logic uses a structured format of categorical propositions and syllogisms based on subject-predicate relationships, primarily involving quantifiers like "all," "some," or "none." Predicate logic expands this structure by introducing predicates that express properties or relations, combined with variables and quantifiers such as (for all) and (there exists), enabling more complex statements. The syntax of predicate logic allows nesting and manipulation of multiple predicates and variables, providing greater expressive power compared to the fixed form of syllogistic categorical statements.
Expressive Power and Limitations
Syllogistic logic, rooted in Aristotelian tradition, offers limited expressive power by handling only categorical propositions and simple reasoning patterns involving quantifiers like "all" or "some." Predicate logic vastly expands this capacity, enabling detailed representation of complex relationships and properties through quantifiers, variables, and predicates, thus capturing nuances beyond syllogistic constraints. The primary limitation of syllogistic logic lies in its inability to express nested or multiple-quantified statements, whereas predicate logic's complexity requires more sophisticated methods for proof and decidability.
Applications of Syllogistic Logic in Reasoning
Syllogistic logic, rooted in Aristotle's framework, applies primarily to categorical reasoning, enabling clear deductions by analyzing relationships between broad classes or categories. It is extensively employed in qualitative analysis, legal reasoning, and ethical debates where straightforward categorical comparisons simplify complex scenarios. The structured form of syllogisms supports decision-making processes that require definitive, rule-based conclusions without the need for quantifiers or complex predicates found in predicate logic.
Predicate Logic in Modern Mathematics and AI
Predicate logic, also known as first-order logic, extends syllogistic logic by incorporating quantifiers and variables, enabling the expression of more complex statements about objects and their properties. In modern mathematics, predicate logic forms the foundation of formal theories and proofs, providing a rigorous framework for defining structures and verifying mathematical truths. Its application in artificial intelligence is pivotal for knowledge representation, automated reasoning, and natural language processing, allowing AI systems to handle nuanced logical inference beyond categorical syllogisms.
Philosophical Implications and Debates
Syllogistic logic, rooted in Aristotelian tradition, emphasizes categorical propositions and their inferential relations, shaping early philosophical understandings of deductive reasoning and ontology. Predicate logic extends beyond syllogisms by incorporating quantifiers and variables, enabling more precise analysis of language, meaning, and existence, which profoundly challenges classical metaphysical assumptions. Philosophical debates center on the adequacy of syllogistic frameworks for capturing logical inference versus the expressive power and formal rigor of predicate logic in representing complex philosophical arguments.
Conclusion: Choosing the Right Logical Framework
Syllogistic logic, rooted in Aristotle's categorical statements, excels in analyzing straightforward categorical relationships but lacks the expressive power to handle complex statements involving multiple quantifiers and relations. Predicate logic expands this framework by incorporating quantifiers and variables, enabling nuanced reasoning across diverse domains such as mathematics, computer science, and linguistics. Selecting the appropriate logical framework depends on the complexity of the problem: syllogistic logic suits simple categorical deductions, while predicate logic offers robust tools for intricate logical analysis and formal proofs.
Syllogistic logic Infographic
 libterm.com
libterm.com