Fuzzy logic enhances decision-making processes by handling uncertainties and imprecise information more effectively than traditional binary logic. It mimics human reasoning by allowing partial truths, which improves various applications from control systems to artificial intelligence. Explore the rest of the article to discover how fuzzy logic can elevate your technology solutions and problem-solving skills.
Table of Comparison
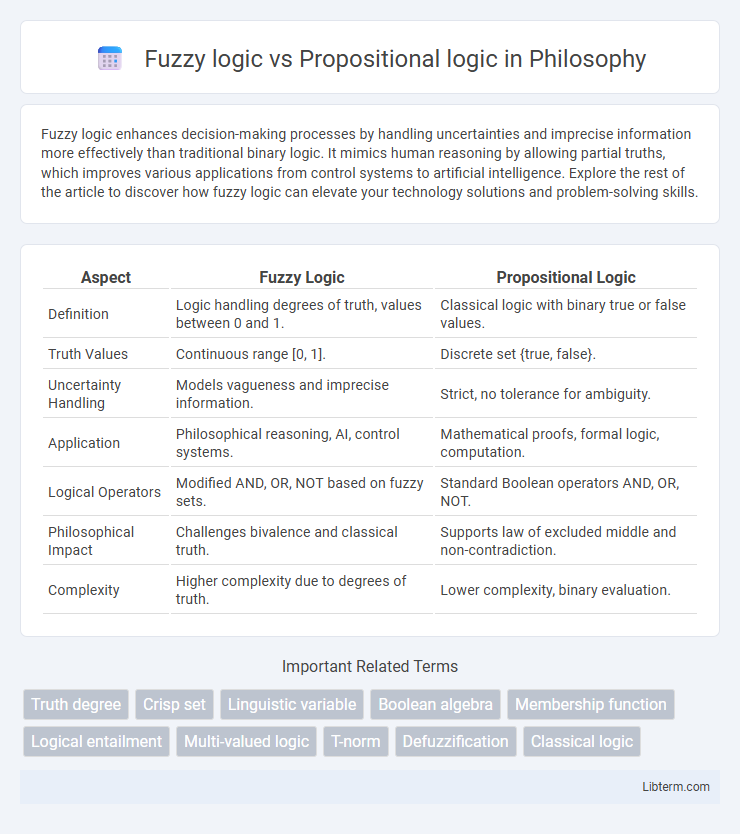
| Aspect | Fuzzy Logic | Propositional Logic |
|---|---|---|
| Definition | Logic handling degrees of truth, values between 0 and 1. | Classical logic with binary true or false values. |
| Truth Values | Continuous range [0, 1]. | Discrete set {true, false}. |
| Uncertainty Handling | Models vagueness and imprecise information. | Strict, no tolerance for ambiguity. |
| Application | Philosophical reasoning, AI, control systems. | Mathematical proofs, formal logic, computation. |
| Logical Operators | Modified AND, OR, NOT based on fuzzy sets. | Standard Boolean operators AND, OR, NOT. |
| Philosophical Impact | Challenges bivalence and classical truth. | Supports law of excluded middle and non-contradiction. |
| Complexity | Higher complexity due to degrees of truth. | Lower complexity, binary evaluation. |
Introduction to Fuzzy Logic and Propositional Logic
Fuzzy logic extends classical propositional logic by allowing truth values to range continuously between 0 and 1, representing degrees of truth rather than binary true or false. Propositional logic operates on discrete propositions with boolean values, enabling precise logical deductions but lacking the ability to handle uncertainty and partial truth. Fuzzy logic is widely applied in control systems, artificial intelligence, and decision-making processes where ambiguity and vagueness are inherent.
Fundamental Concepts of Propositional Logic
Propositional logic, also known as Boolean logic, centers on statements that are either true or false, represented by propositions and combined using logical connectives like AND, OR, and NOT. It relies on binary truth values, enabling precise and deterministic reasoning through well-defined syntax and semantics. This framework contrasts with fuzzy logic, which allows for degrees of truth between 0 and 1, enabling more flexible handling of uncertainty and partial truth in complex problem-solving.
Core Principles of Fuzzy Logic
Fuzzy logic operates on the principle of partial truth values between completely true and completely false, allowing for reasoning with uncertainty and imprecision unlike propositional logic's binary true/false framework. It employs membership functions to quantify the degree to which an element belongs to a set, enabling nuanced decision-making in complex systems. This core principle of graded truth degrees makes fuzzy logic particularly effective for modeling real-world scenarios with ambiguous or overlapping data.
Differences in Truth Values: Boolean vs. Degrees
Fuzzy logic differs from propositional logic primarily in its treatment of truth values, where propositional logic relies on Boolean values strictly defined as true or false (1 or 0). In contrast, fuzzy logic allows for degrees of truth, represented by any value between 0 and 1, capturing uncertainty and partial truth more effectively. This flexibility enables fuzzy logic to model real-world scenarios with vagueness, unlike rigid binary evaluations in propositional logic.
Expressiveness and Application Scope
Fuzzy logic offers greater expressiveness by handling degrees of truth between completely true and false, making it ideal for modeling uncertainty and imprecise information in real-world scenarios such as control systems and decision-making. Propositional logic, with its binary true/false values, excels in applications requiring clear-cut, definitive reasoning like digital circuit design and formal verification. The broader application scope of fuzzy logic spans areas involving human-like reasoning and approximate inference, whereas propositional logic is confined to strict, well-defined problem domains.
Handling Uncertainty and Vagueness
Fuzzy logic effectively handles uncertainty and vagueness by allowing truth values to range continuously between 0 and 1, representing degrees of truth rather than binary true/false values inherent in propositional logic. This continuous spectrum enables fuzzy logic to model real-world scenarios with ambiguous or imprecise data more accurately than propositional logic, which is limited to crisp, well-defined true or false propositions. Consequently, fuzzy logic is widely applied in fields such as control systems, decision-making, and natural language processing where uncertainty and partial truth are predominant.
Real-World Applications: Fuzzy vs. Propositional Logic
Fuzzy logic excels in real-world applications requiring nuanced decision-making and uncertainty management, such as climate control systems, medical diagnosis, and autonomous vehicles, due to its ability to handle partial truths and approximate reasoning. Propositional logic, while effective in precise and deterministic systems like digital circuit design and formal verification, struggles with ambiguity and incomplete information. The adaptability of fuzzy logic makes it more suitable for dynamic environments where human-like reasoning is essential, contrasting with the rigid true/false framework of propositional logic.
Advantages and Limitations of Propositional Logic
Propositional logic offers clear advantages such as simplicity, ease of implementation, and precise truth values that enable straightforward reasoning in binary systems. However, its limitations include inability to handle uncertainty, partial truths, or graded information, which restricts its use in real-world scenarios with ambiguous or incomplete data. These constraints make propositional logic less flexible compared to fuzzy logic, which excels in managing vagueness and complex decision-making processes.
Strengths and Weaknesses of Fuzzy Logic
Fuzzy logic excels in handling uncertainty and imprecision by allowing degrees of truth rather than binary true/false values, making it ideal for real-world applications like control systems and decision-making under ambiguity. Its main strength lies in modeling complex systems with vagueness, unlike propositional logic which strictly adheres to Boolean values and struggles with partial truths. However, fuzzy logic's weakness includes increased computational complexity and lack of universality in formal proof systems, limiting its effectiveness in purely mathematical or deterministic contexts.
Choosing Between Fuzzy Logic and Propositional Logic
Fuzzy logic excels in handling uncertainty and imprecision by modeling degrees of truth, making it ideal for complex decision-making and control systems where binary true/false values are insufficient. Propositional logic provides clear, strict true or false evaluations, suited for applications requiring precise, unequivocal reasoning, such as formal verification and digital circuit design. Selecting between fuzzy logic and propositional logic depends on the need for nuanced truth representation versus exact binary conditions in the target problem domain.
Fuzzy logic Infographic
 libterm.com
libterm.com