Intuitionistic logic focuses on constructive proofs where the truth of a statement is demonstrated by explicitly constructing a proof rather than relying on classical principles like the law of excluded middle. This form of logic is fundamental in fields such as computer science and mathematical constructivism, emphasizing how information is built step-by-step. Explore the rest of the article to deepen your understanding of intuitionistic logic and its applications.
Table of Comparison
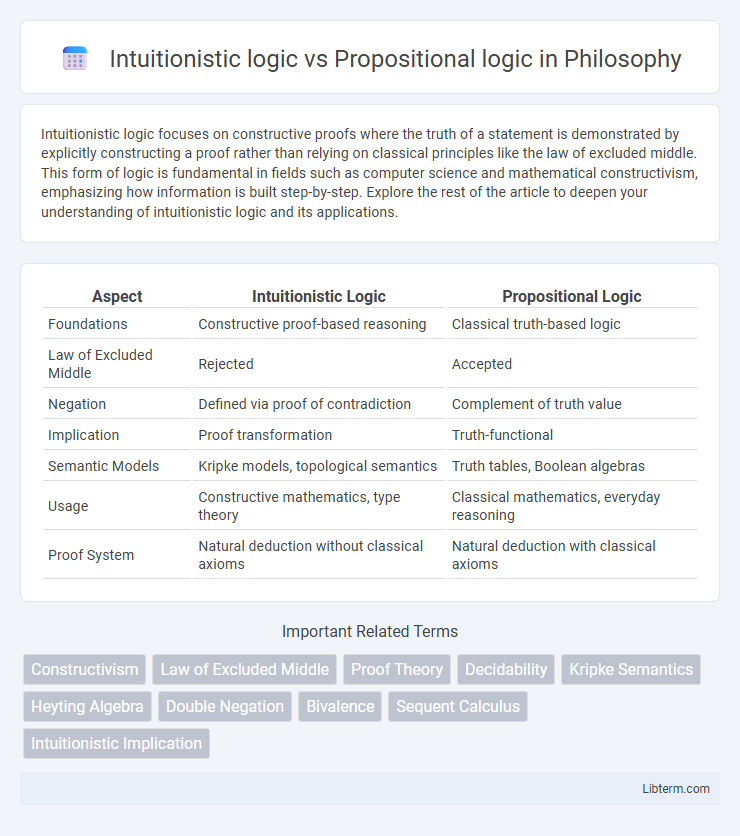
| Aspect | Intuitionistic Logic | Propositional Logic |
|---|---|---|
| Foundations | Constructive proof-based reasoning | Classical truth-based logic |
| Law of Excluded Middle | Rejected | Accepted |
| Negation | Defined via proof of contradiction | Complement of truth value |
| Implication | Proof transformation | Truth-functional |
| Semantic Models | Kripke models, topological semantics | Truth tables, Boolean algebras |
| Usage | Constructive mathematics, type theory | Classical mathematics, everyday reasoning |
| Proof System | Natural deduction without classical axioms | Natural deduction with classical axioms |
Introduction to Intuitionistic and Propositional Logic
Intuitionistic logic, unlike classical propositional logic, rejects the law of excluded middle, emphasizing constructive proof and verification over mere truth values. Propositional logic operates under bivalent truth values--true or false--while intuitionistic logic interprets propositions through the existence of constructive evidence. This foundational difference impacts proof theory and computational interpretations, making intuitionistic logic essential in areas like type theory and programming language semantics.
Historical Background and Development
Propositional logic, dating back to Aristotle's syllogistic logic, was formalized in the late 19th century through the work of Frege and Russell, establishing classical truth-functional frameworks. Intuitionistic logic emerged in the early 20th century by L.E.J. Brouwer as part of the intuitionism movement, rejecting the law of excluded middle and emphasizing constructive proof methods. The development of intuitionistic logic was motivated by foundational concerns in mathematics, contrasting classical propositional logic's acceptance of non-constructive proofs and influencing subsequent studies in proof theory and type theory.
Fundamental Principles and Key Differences
Intuitionistic logic, rooted in constructivist mathematics, rejects the law of excluded middle, emphasizing proof construction rather than truth value assignment, contrasting with classical propositional logic which accepts bivalence and uses truth tables. Intuitionistic logic's semantic framework employs Kripke models whereas propositional logic relies on classical Boolean valuations. Key differences include the interpretation of negation and implication, where intuitionistic logic requires explicit construction of evidence, altering proof techniques and logical derivations.
Syntax and Semantic Structures
Intuitionistic logic differs from propositional logic primarily in its semantic structure, rejecting the law of excluded middle and emphasizing constructive proof principles. Its syntax retains standard propositional operators such as conjunction, disjunction, and implication but interprets them through Heyting algebras rather than Boolean algebras. This shift in semantic foundation leads to a calculus where truth values are not binary but reflect proof existence, profoundly impacting the formulation and validation of logical statements.
Truth Values: Classical vs. Intuitionistic Perspectives
Intuitionistic logic interprets truth values constructively, where a proposition is true only if there is a proof, contrasting with classical propositional logic that assigns a binary truth value: true or false. In classical logic, the law of excluded middle (P !P) holds universally, whereas intuitionistic logic rejects this law unless a proof of either P or !P is available. This difference leads to intuitionistic semantics using Kripke models or Heyting algebras to represent truth as a growing evidence-based notion instead of static binary states.
The Law of Excluded Middle in Both Logics
The Law of Excluded Middle states that for any proposition P, either P or not-P must be true. In propositional logic, this principle is universally accepted and forms a foundational axiom, ensuring classical binary truth values. Intuitionistic logic rejects the Law of Excluded Middle, requiring constructive proof of either P or not-P, thus making truth dependent on verifiable evidence rather than abstract binary assignments.
Applications and Use Cases
Intuitionistic logic is pivotal in type theory and constructive mathematics, enabling proofs that guarantee the existence of explicit witnesses, crucial in programming language design and formal verification. Propositional logic excels in classical automated theorem proving, digital circuit design, and knowledge representation, where binary truth values facilitate efficient computation and decision-making. Both logics underpin artificial intelligence, with intuitionistic logic enhancing reasoning in systems requiring constructive proofs, while propositional logic supports fast logical inference in rule-based expert systems.
Proof Techniques and Constructive Reasoning
Intuitionistic logic emphasizes constructive reasoning by requiring explicit proof of existence and disallowing the law of excluded middle, contrasting with classical propositional logic's acceptance of non-constructive proof methods. Proof techniques in intuitionistic logic rely heavily on the construction of witnesses and the use of natural deduction systems that avoid classical principles such as double negation elimination. This constructive framework aligns with computational interpretations, making intuitionistic logic foundational in fields like type theory and programming language semantics.
Advantages and Limitations
Intuitionistic logic offers advantages in constructive mathematics by emphasizing proof existence rather than mere truth, enabling more computationally meaningful interpretations compared to classical propositional logic. However, its limitation lies in rejecting the law of excluded middle, which restricts some classical reasoning techniques and can complicate proofs that rely on non-constructive methods. Propositional logic, while more broadly applicable with simpler semantic rules, lacks the constructive guarantees and finer expressive power inherent to intuitionistic frameworks.
Conclusion and Future Directions
Intuitionistic logic, rejecting the law of the excluded middle, demands constructive proof methods, contrasting sharply with classical propositional logic's binary truth evaluation. Advancements in type theory and proof assistants are poised to leverage intuitionistic frameworks for enhanced formal verification and constructive mathematics. Future research may emphasize integrating intuitionistic logic with computational paradigms, improving automated reasoning, and expanding applications in secure programming languages.
Intuitionistic logic Infographic
 libterm.com
libterm.com