Higher-order logic extends classical first-order logic by allowing quantification not only over individuals but also over predicates, functions, and sets, significantly enhancing expressive power for formal reasoning. This increased expressiveness makes it a crucial tool in areas such as mathematics, computer science, and artificial intelligence for representing and solving complex problems. Discover how higher-order logic can deepen your understanding of formal systems and their applications by exploring the rest of this article.
Table of Comparison
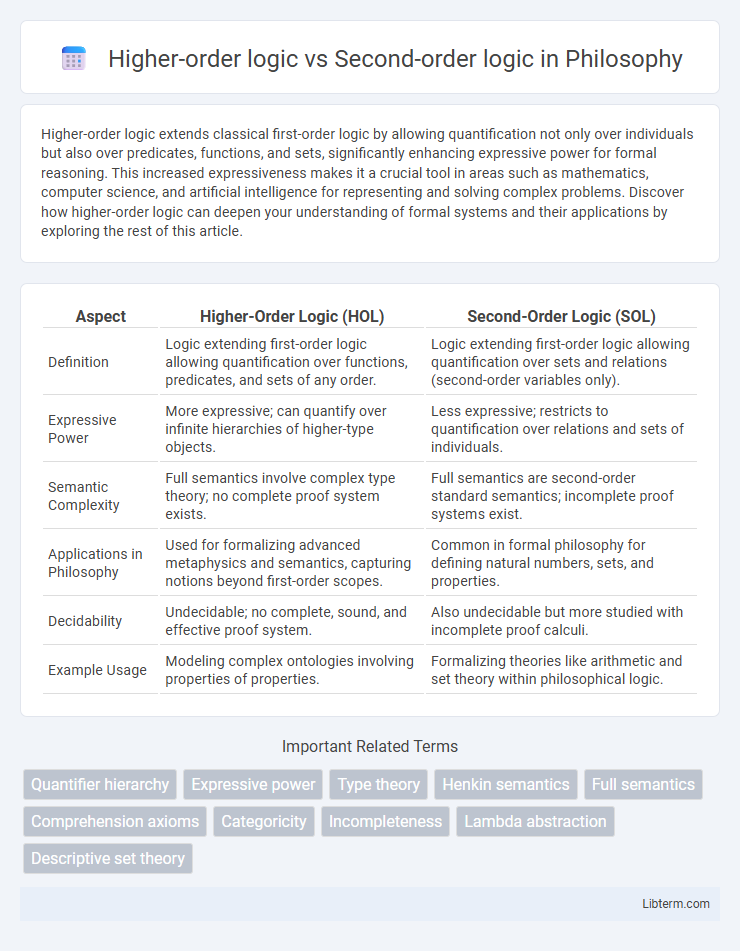
| Aspect | Higher-Order Logic (HOL) | Second-Order Logic (SOL) |
|---|---|---|
| Definition | Logic extending first-order logic allowing quantification over functions, predicates, and sets of any order. | Logic extending first-order logic allowing quantification over sets and relations (second-order variables only). |
| Expressive Power | More expressive; can quantify over infinite hierarchies of higher-type objects. | Less expressive; restricts to quantification over relations and sets of individuals. |
| Semantic Complexity | Full semantics involve complex type theory; no complete proof system exists. | Full semantics are second-order standard semantics; incomplete proof systems exist. |
| Applications in Philosophy | Used for formalizing advanced metaphysics and semantics, capturing notions beyond first-order scopes. | Common in formal philosophy for defining natural numbers, sets, and properties. |
| Decidability | Undecidable; no complete, sound, and effective proof system. | Also undecidable but more studied with incomplete proof calculi. |
| Example Usage | Modeling complex ontologies involving properties of properties. | Formalizing theories like arithmetic and set theory within philosophical logic. |
Introduction to Higher-Order and Second-Order Logic
Higher-order logic (HOL) extends second-order logic by allowing quantification over predicates, functions, and sets of arbitrary order, enabling more expressive formalization of mathematical statements. Second-order logic quantifies only over sets or relations of individual elements, providing a robust framework for formal semantics but with limitations compared to HOL's comprehensive scope. Both logics serve foundational roles in formal verification, knowledge representation, and type theory, with HOL offering greater expressive power at the cost of increased complexity.
Historical Background and Development
Higher-order logic (HOL) evolved from the limitations of second-order logic (SOL) in capturing complex mathematical concepts, with its origins traced back to the early 20th century during the formalization efforts of logic by Frege and Russell. Second-order logic gained prominence through its ability to quantify not only over individual variables but also over sets and relations, distinguishing it from first-order logic and influencing the development of model theory. The progression from second-order to higher-order logic involved extending quantification to functions and predicates of higher types, driven by the work of Church and others in the mid-20th century, which laid the foundation for modern type theory and automated theorem proving.
Syntax and Semantics Overview
Higher-order logic (HOL) extends second-order logic (SOL) by allowing quantification not only over sets and relations but also over functions and predicates of any finite type, leading to a richer syntax with more complex type hierarchies. The semantics of HOL are often interpreted using full type theory models, which provide precise meanings for all higher-type variables, whereas SOL semantics typically involve standard models with quantification restricted to subsets or relations on the domain. Syntax in SOL is limited to quantification over elements and subsets of the domain, making it less expressive but simpler than HOL, which supports a broader range of logical constructs through its layered typing system.
Expressive Power: Comparing Capabilities
Higher-order logic (HOL) surpasses second-order logic (SOL) in expressive power by allowing quantification over predicates of any finite order, not just sets and relations. This enables HOL to represent more complex mathematical concepts and properties that SOL cannot capture, such as statements involving functions over functions or predicates over predicates. Consequently, HOL provides a richer framework for formalizing theories and conducting advanced reasoning beyond the scope of SOL's capabilities.
Decidability and Completeness
Higher-order logic (HOL) extends second-order logic by allowing quantification over functions and predicates of any order, resulting in greater expressiveness but increased complexity in decidability and completeness. Second-order logic is semi-decidable and lacks a complete, sound, and effective proof system, similar to HOL, yet HOL's undecidability is more acute due to its broader quantificational scope. Both logics are not recursively enumerable, with completeness theorems holding only in restricted fragments, making them unsuitable for fully decidable, complete systems in general.
Applications in Mathematics and Computer Science
Higher-order logic extends second-order logic by allowing quantification over predicates of any order, enabling more expressive frameworks for formalizing complex mathematical theories and computer science concepts such as type theory and formal verification. Second-order logic is widely used in descriptive complexity and finite model theory, providing powerful tools for characterizing complexity classes and database theory. Applications in computer science involve formal verification, automated theorem proving, and knowledge representation, where higher-order logic supports more sophisticated reasoning about functions and predicates compared to second-order logic.
Model Theory: Semantics and Interpretations
Higher-order logic (HOL) extends second-order logic (SOL) by allowing quantification over predicates of all finite orders, enabling more expressive semantics in model theory with richer interpretations of higher-type variables. Second-order logic restricts quantification to subsets and relations over individuals, yielding semantics that balance expressive power and interpretability within standard models. In model theory, HOL semantics often require Henkin or general models to accommodate its increased complexity, whereas SOL semantics can be standard or Henkin, but both differ in how interpretations assign meanings to higher-type constructs.
Philosophical and Foundational Implications
Higher-order logic extends second-order logic by allowing quantification over predicates of predicates, increasing expressive power but raising complexity issues. Philosophically, higher-order logic challenges the boundaries of formal systems, as it embraces richer ontologies that second-order logic cannot capture, influencing debates on realism and Platonism in mathematics. Foundationally, while second-order logic is often seen as a robust framework for categorizing mathematical structures, higher-order logic pushes the limits of completeness and decidability, impacting the development of formal foundations for mathematics.
Limitations and Challenges
Higher-order logic (HOL) extends beyond second-order logic (SOL) by allowing quantification over functions and predicates of all orders, but this increased expressiveness introduces significant undecidability and complexity challenges, making automated reasoning more difficult. Second-order logic, while more expressive than first-order logic by quantifying over sets, is limited by its lack of completeness and the non-existence of a sound and complete proof system for full semantics. Both HOL and SOL face limitations in their practical application due to these foundational trade-offs between expressiveness and decidability, complicating their use in formal verification and theorem proving.
Conclusion: Choosing Between Higher-Order and Second-Order Logic
Higher-order logic encompasses second-order logic as a subset but extends beyond it by allowing quantification over functions and predicates of all orders, offering greater expressiveness at the cost of increased complexity and reduced decidability. Second-order logic balances expressiveness and complexity, providing powerful tools for formalizing mathematics with better-understood semantics and more manageable proof systems. Choosing between higher-order and second-order logic depends on the specific requirements for expressiveness versus tractability in logical reasoning and formal verification contexts.
Higher-order logic Infographic
 libterm.com
libterm.com