Asymmetry plays a crucial role in design, art, and nature by creating visual interest and dynamic balance without the need for perfect symmetry. It challenges traditional notions of harmony, offering unique compositions that draw the viewer's eye and evoke emotional responses. Discover how asymmetry can transform your creative projects and enhance aesthetic appeal in the rest of this article.
Table of Comparison
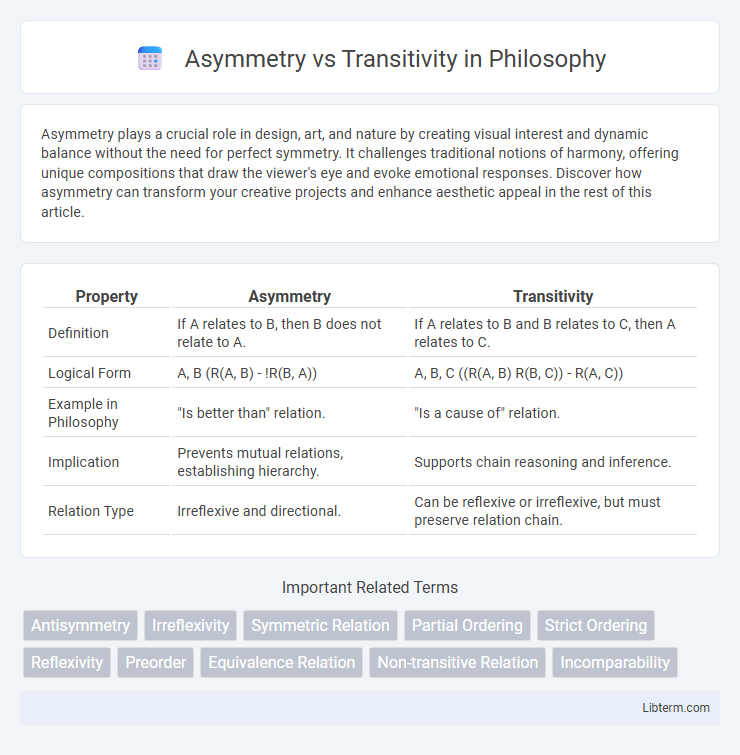
| Property | Asymmetry | Transitivity |
|---|---|---|
| Definition | If A relates to B, then B does not relate to A. | If A relates to B and B relates to C, then A relates to C. |
| Logical Form | A, B (R(A, B) - !R(B, A)) | A, B, C ((R(A, B) R(B, C)) - R(A, C)) |
| Example in Philosophy | "Is better than" relation. | "Is a cause of" relation. |
| Implication | Prevents mutual relations, establishing hierarchy. | Supports chain reasoning and inference. |
| Relation Type | Irreflexive and directional. | Can be reflexive or irreflexive, but must preserve relation chain. |
Understanding Asymmetry: Definition and Examples
Asymmetry in relations occurs when a relationship between two elements only holds in one direction, meaning if element A relates to element B, then B cannot relate to A in the same way; for example, the relation "is a parent of" is asymmetric because if person A is a parent of person B, person B cannot be a parent of person A. Understanding asymmetry involves recognizing that such relations do not allow reciprocal connections, distinguishing them from symmetric or bidirectional relations. This concept plays a crucial role in fields like logic, mathematics, and computer science, where directional relationships must be clearly defined and analyzed.
Exploring Transitivity: Meaning and Real-World Cases
Transitivity refers to a property of relations where if a relation holds between A and B, and between B and C, it must also hold between A and C, as seen in equality or subset relations. Real-world examples include social networks where if person A trusts person B, and person B trusts person C, transitivity implies person A may trust person C. Understanding transitivity allows for modeling complex systems like recommendation algorithms or hierarchical classifications effectively.
Core Differences Between Asymmetry and Transitivity
Asymmetry refers to a binary relation where if an element a relates to b, then b cannot relate to a, exemplified by the "less than" relation (<), which is irreflexive and one-directional. Transitivity, on the other hand, involves a relation where if a relates to b and b relates to c, then a must relate to c, as seen in the "less than or equal to" relation (<=), which can be reflexive. The core difference lies in asymmetry prohibiting mutual relationships between pairs, while transitivity focuses on the preservation of a relation through chains of elements.
Mathematical Representation of Asymmetry and Transitivity
Asymmetry in mathematical relations is defined such that if an element a is related to b, then b is not related to a, formally expressed as a, b (R(a, b) - !R(b, a)). Transitivity requires that whenever a is related to b and b is related to c, then a must be related to c, denoted as a, b, c ((R(a, b) R(b, c)) - R(a, c)). These properties are fundamental in defining strict partial orders and equivalence relations within set theory and graph theory.
Asymmetry vs Transitivity in Logic Relations
Asymmetry in logic relations occurs when a relation R satisfies the condition that if R(a, b) holds, then R(b, a) does not hold, such as the "less than" relation (<). Transitivity requires that whenever R(a, b) and R(b, c) are true, R(a, c) must also be true, exemplified by the "ancestor of" relation. In logic, these properties interact crucially; for instance, strict partial orders are characterized by asymmetry and transitivity, whereas a relation may be transitive without being asymmetric, highlighting distinct structural constraints within formal relational systems.
Applications of Asymmetry in Computer Science
Asymmetry plays a crucial role in computer science, particularly in the design of data structures and algorithms where directionality matters, such as in directed graphs and priority queues. It enables modeling relationships where reciprocity does not hold, essential for authorization systems, access control, and dependency resolution. Applications extend to database indexing, network routing protocols, and cryptographic functions where asymmetric properties ensure security and efficiency.
Significance of Transitivity in Data Analysis
Transitivity plays a crucial role in data analysis by ensuring consistent relationships within datasets, which simplifies complex network structures and improves inferential accuracy. Unlike asymmetry, transitive properties enable the inference of indirect connections, enhancing the robustness of clustering algorithms and graph-based models. Efficient utilization of transitivity leads to better pattern recognition, anomaly detection, and predictive analytics across domains such as social network analysis, recommendation systems, and hierarchical classification.
Common Misconceptions: Asymmetry vs Transitivity
Asymmetry and transitivity are often confused in logic, but they describe different properties of relations. Asymmetry means if a relation holds from A to B, it cannot hold from B to A, while transitivity means if a relation holds from A to B and B to C, it must hold from A to C. A common misconception is assuming that all asymmetric relations are transitive or that transitive relations must be asymmetric, which is not necessarily true in formal logic.
Importance in Social and Biological Networks
Asymmetry in social and biological networks highlights directional relationships, such as dominance hierarchies or information flow, emphasizing the unequal influence between nodes. Transitivity reflects the tendency for interconnected nodes to form cohesive clusters, crucial for community stability and cooperation. Understanding the balance between asymmetry and transitivity enables better modeling of network dynamics, revealing how influence spreads and groups organize in complex systems.
Summary: Choosing Between Asymmetry and Transitivity
Choosing between asymmetry and transitivity depends on the nature of the relation being modeled, as asymmetry requires that if a relation holds from entity A to B, it cannot hold from B to A, while transitivity ensures if it holds from A to B and B to C, it also holds from A to C. In systems like preference orderings, asymmetry prevents mutual preference contradictions, whereas transitivity maintains consistent ordering across multiple elements. Balancing these properties is crucial in fields such as mathematics, linguistics, and computer science to accurately capture relational structures and avoid logical inconsistencies.
Asymmetry Infographic
 libterm.com
libterm.com