Symmetry plays a crucial role in both natural and human-made designs, offering balance and harmony that appeal to the eye and mind. It enhances visual aesthetics and contributes to structural stability in architecture, art, and nature. Discover how understanding the principles of symmetry can transform your perception and approach by reading the rest of this article.
Table of Comparison
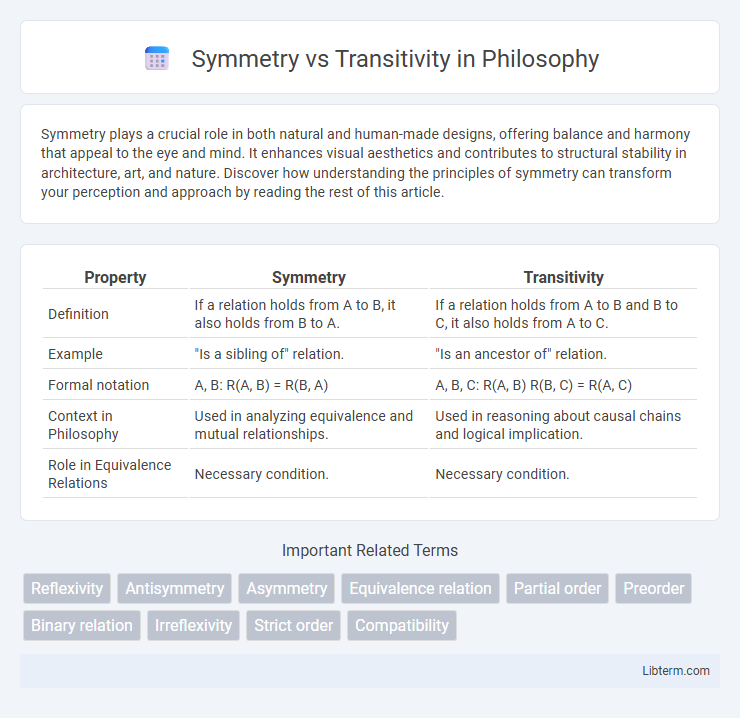
| Property | Symmetry | Transitivity |
|---|---|---|
| Definition | If a relation holds from A to B, it also holds from B to A. | If a relation holds from A to B and B to C, it also holds from A to C. |
| Example | "Is a sibling of" relation. | "Is an ancestor of" relation. |
| Formal notation | A, B: R(A, B) = R(B, A) | A, B, C: R(A, B) R(B, C) = R(A, C) |
| Context in Philosophy | Used in analyzing equivalence and mutual relationships. | Used in reasoning about causal chains and logical implication. |
| Role in Equivalence Relations | Necessary condition. | Necessary condition. |
Introduction to Symmetry and Transitivity
Symmetry in mathematics refers to a relation where if element A is related to element B, then B is also related to A, as seen in symmetric relations like equality and friendship. Transitivity describes a relation where if element A is related to B, and B to C, then A must be related to C, which is crucial in ordering and equivalence relations. Understanding these properties is key for analyzing the structure and behavior of relations in set theory, algebra, and logic.
Defining Symmetry in Mathematical Relations
Symmetry in mathematical relations occurs when a relation R on a set satisfies the condition that if an element a is related to an element b, then b is also related to a. Formally, a relation R is symmetric if for every (a, b) in R, the pair (b, a) is also in R. This property contrasts with transitivity, where the relation requires consecutive related pairs to imply a direct relation between the first and third elements.
Understanding Transitivity in Relations
Transitivity in relations ensures that if a relation holds between a first element and a second, and also between the second and a third, then it must hold between the first and third. This property is fundamental in mathematical structures such as equivalence relations and partial orders, enabling consistent chaining of related elements. Understanding transitivity helps in analyzing systems where indirect connections imply direct relationships, such as social networks, preference rankings, and graph theory.
Key Differences Between Symmetry and Transitivity
Symmetry refers to a relation where if element A is related to element B, then element B is also related to element A, exemplified by equality or friendship relations. Transitivity implies that if element A is related to element B and element B is related to element C, then element A must be related to element C, seen in orderings like "less than or equal to." The key difference lies in symmetry requiring mutual relationships between pairs, while transitivity ensures a consistent chain of relations across triples.
Symmetric Relations: Examples and Properties
Symmetric relations occur when for any elements a and b in a set, if a is related to b, then b is also related to a, such as in the relation "is a sibling of" or "is married to." These relations exhibit the property that swapping the pair does not affect the relation's truth, crucial in equivalence relations alongside reflexivity and transitivity. Understanding symmetric relations aids in modeling mutual connections in graph theory, social networks, and equivalence classes in algebra.
Transitive Relations: Examples and Characteristics
Transitive relations occur when a relation between elements maintains consistency through a chain, meaning if element A relates to B and B relates to C, then A must relate to C. Classic examples include the "less than" relation on numbers, where if 3 < 5 and 5 < 7, it follows that 3 < 7, and the subset relation in set theory, where if set A is a subset of B and B is a subset of C, then A is a subset of C. Transitive relations are characterized by their ability to combine relations across multiple pairs, forming a logical bridge that preserves the relation through linkage.
Importance of Symmetry and Transitivity in Mathematics
Symmetry and transitivity are fundamental properties in mathematics that underpin the behavior of relations and structures such as equivalence relations and orderings. Symmetry ensures that relationships are mutually consistent, as seen in congruence and equality, while transitivity guarantees the logical flow and coherence across elements, critical in ordering sets or proving theorems. The combined importance of symmetry and transitivity enables the formation of equivalence classes and ordered partitions, which are essential in various mathematical fields including algebra, geometry, and logic.
Applications of Symmetry and Transitivity in Real Life
Symmetry plays a critical role in fields like physics, where it underpins conservation laws and particle interactions, and in design and architecture, ensuring aesthetic balance and structural stability. Transitivity is essential in decision-making and data sorting algorithms, enabling consistent ranking and classification systems used in economics, social sciences, and computer science. Both properties contribute to efficient problem-solving and reasoning within various logical frameworks and practical scenarios.
Common Misconceptions: Symmetry vs Transitivity
Symmetry and transitivity are often confused properties in relation to binary relations, but they describe fundamentally different behaviors. Symmetry requires that if an element a is related to b, then b must also be related to a, exemplified by equality and friendship in social networks. Transitivity demands that if a is related to b and b to c, then a must be related to c, as seen in the mathematical "less than or equal to" relation, highlighting the common misconception that symmetry implies transitivity or vice versa.
Summary and Conclusion
Symmetry in relations means if element A is related to element B, then B is also related to A, while transitivity requires that if A is related to B and B is related to C, then A must be related to C. These properties define distinct but fundamental aspects of mathematical and logical relations, crucial for understanding equivalence relations and order relations. Recognizing the difference between symmetry and transitivity helps clarify the structure and behavior of various relational systems in mathematics and computer science.
Symmetry Infographic
 libterm.com
libterm.com