Nonlinear systems exhibit behaviors that cannot be explained by simple proportionality, leading to complex and often unpredictable outcomes. These systems are prevalent in various fields such as physics, economics, and biology, where small changes in input can cause significant differences in results. Explore the rest of this article to understand how nonlinear dynamics influence your everyday experiences and decision-making processes.
Table of Comparison
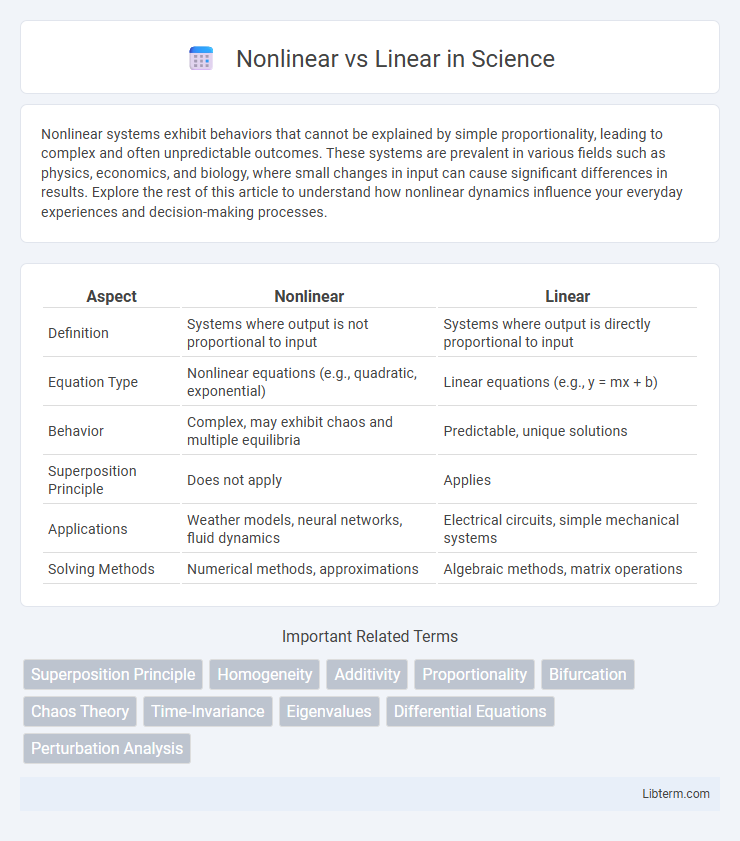
| Aspect | Nonlinear | Linear |
|---|---|---|
| Definition | Systems where output is not proportional to input | Systems where output is directly proportional to input |
| Equation Type | Nonlinear equations (e.g., quadratic, exponential) | Linear equations (e.g., y = mx + b) |
| Behavior | Complex, may exhibit chaos and multiple equilibria | Predictable, unique solutions |
| Superposition Principle | Does not apply | Applies |
| Applications | Weather models, neural networks, fluid dynamics | Electrical circuits, simple mechanical systems |
| Solving Methods | Numerical methods, approximations | Algebraic methods, matrix operations |
Introduction to Linear and Nonlinear Systems
Linear systems are characterized by proportional input-output relationships and adhere to the principle of superposition, making them predictable and easier to analyze using methods like Laplace transforms and matrix algebra. Nonlinear systems exhibit output responses that are not directly proportional to inputs, often leading to complex behaviors such as chaos, bifurcations, and limit cycles, which require specialized techniques like phase plane analysis and numerical simulations. Understanding these fundamental differences is crucial for accurately modeling physical, biological, and engineering processes.
Defining Linear Systems
Linear systems are characterized by the principles of superposition and homogeneity, where the output response is directly proportional to the input signal. Such systems maintain additive and scaling properties, allowing predictable and straightforward mathematical modeling through linear differential equations. In contrast, nonlinear systems exhibit outputs that are not directly proportional to inputs, leading to complex behaviors such as chaos and multiple equilibrium points.
Defining Nonlinear Systems
Nonlinear systems are defined by equations in which the output is not directly proportional to the input, often resulting in complex behavior such as chaos and bifurcations. Unlike linear systems that follow the principle of superposition, nonlinear systems involve interactions that cannot be expressed as a simple sum of their components. Key characteristics of nonlinear dynamics include sensitivity to initial conditions and the presence of multiple equilibrium points or limit cycles.
Key Differences Between Linear and Nonlinear Models
Linear models assume a direct proportionality between input variables and output, represented by a straight-line relationship, making them easier to interpret and computationally efficient. Nonlinear models capture complex, curved relationships where output changes are not proportional to inputs, allowing for greater flexibility in modeling real-world phenomena but requiring more computational power and data. Key differences include interpretability, computational complexity, and the ability to model interactions and varying effects within nonlinear frameworks versus the simplicity and stability of linear models.
Mathematical Representation of Linear vs Nonlinear Equations
Linear equations are mathematically represented by expressions where variables appear to the power of one and their graphs form straight lines, typically in the form ax + by = c. Nonlinear equations involve variables raised to powers other than one or multiplied together, producing curves, surfaces, or more complex geometric figures. This fundamental difference in mathematical representation directly influences solution methods and the complexity of analyzing system behavior.
Real-World Applications of Linear Systems
Linear systems underpin numerous real-world applications due to their predictable behavior and ease of analysis, such as electrical circuit design, control systems, and signal processing. In engineering, linear models simplify the study of mechanical vibrations and thermal conduction, providing accurate approximations for many practical problems. Their mathematical properties enable efficient computational methods, essential for optimization in economics, robotics, and communications.
Real-World Applications of Nonlinear Systems
Nonlinear systems exhibit complex behaviors such as chaos, bifurcations, and multiple equilibria, making them essential in modeling phenomena like weather patterns, population dynamics, and financial markets. Linear systems, defined by proportionality and additivity, simplify analysis but often fail to capture real-world intricacies present in engineering, biology, and economics. The nonlinear approach is critical in designing control systems, predicting climate change, and understanding neural network operations, where interactions and feedback loops generate unpredictable, dynamic responses.
Advantages and Limitations of Linear Systems
Linear systems offer simplicity in analysis and design due to their proportionality and superposition properties, enabling predictable and efficient solutions in engineering and control applications. Their limitations include the inability to accurately model complex real-world phenomena involving nonlinear interactions, such as saturation, hysteresis, or chaotic dynamics. Despite constraints, linear systems remain fundamental for approximating behavior near equilibrium points and serving as a foundation for more advanced nonlinear system analysis.
Advantages and Limitations of Nonlinear Systems
Nonlinear systems offer advantages such as the ability to model complex, real-world phenomena with greater accuracy, capturing behaviors like chaos, bifurcations, and saturation effects that linear systems cannot. These systems enable adaptive control in robotics, improved signal processing, and advanced financial modeling but often require intensive computational resources and sophisticated algorithms for analysis and prediction. Limitations include difficulties in solving nonlinear equations explicitly, challenges in stability assessment, and the potential for unpredictable or sensitive dependence on initial conditions, complicating practical implementation.
Choosing Between Linear and Nonlinear Approaches
Choosing between linear and nonlinear approaches hinges on data complexity and model interpretability requirements. Linear methods offer simplicity and ease of interpretation, best suited for datasets exhibiting proportional relationships and minimal interaction effects. Nonlinear techniques excel in capturing intricate patterns and interactions within data, making them ideal for complex systems where linear assumptions fail to hold true.
Nonlinear Infographic
 libterm.com
libterm.com