Field work offers invaluable hands-on experience that deepens your understanding of theoretical concepts and enhances practical skills essential for professional growth. Exposure to real-world environments helps develop problem-solving abilities and adaptability in diverse situations. Explore the full article to discover how engaging in field activities can transform your expertise and career prospects.
Table of Comparison
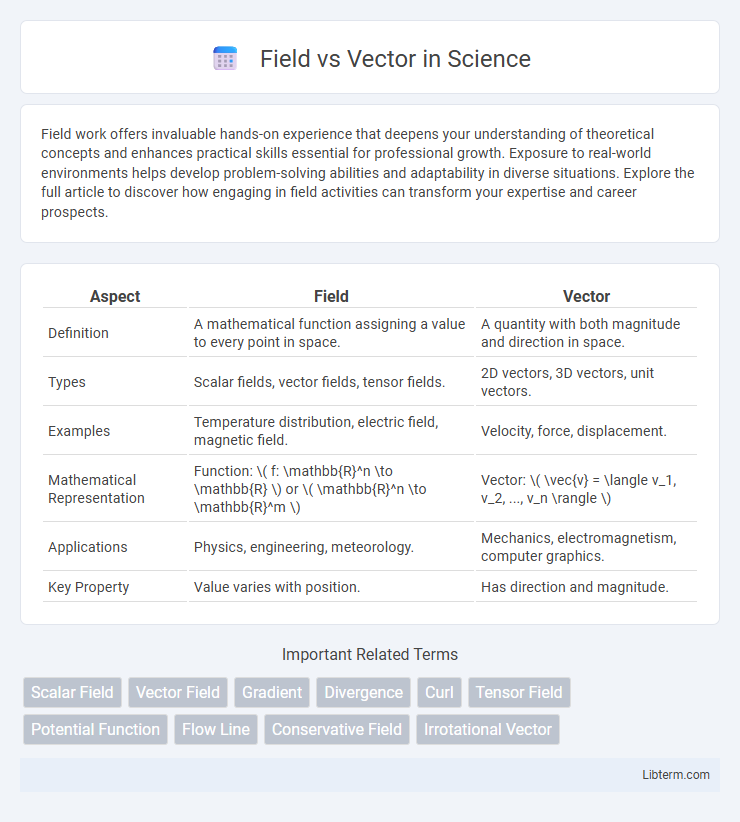
| Aspect | Field | Vector |
|---|---|---|
| Definition | A mathematical function assigning a value to every point in space. | A quantity with both magnitude and direction in space. |
| Types | Scalar fields, vector fields, tensor fields. | 2D vectors, 3D vectors, unit vectors. |
| Examples | Temperature distribution, electric field, magnetic field. | Velocity, force, displacement. |
| Mathematical Representation | Function: \( f: \mathbb{R}^n \to \mathbb{R} \) or \( \mathbb{R}^n \to \mathbb{R}^m \) | Vector: \( \vec{v} = \langle v_1, v_2, ..., v_n \rangle \) |
| Applications | Physics, engineering, meteorology. | Mechanics, electromagnetism, computer graphics. |
| Key Property | Value varies with position. | Has direction and magnitude. |
Understanding the Concept of Field
A field in mathematics or physics assigns a value to every point in space, representing quantities like temperature, pressure, or gravitational force. Unlike a vector, which has both magnitude and direction at a specific point, a scalar field provides only magnitude without direction. Understanding the concept of a field is crucial for analyzing spatial variations of physical phenomena and forms the foundation for vector fields, where each point has a vector quantity.
Defining a Vector in Mathematics
A vector in mathematics is defined as an element of a vector space characterized by both magnitude and direction, distinguishable from a scalar field that assigns a single value to every point in a region. Unlike fields, which can be scalar or vector-valued functions varying over a domain, vectors adhere to operations of vector addition and scalar multiplication within their vector space. This foundational concept enables applications in physics and engineering where vectors represent quantities such as force and velocity with defined directional properties.
Key Differences Between Field and Vector
A field assigns a scalar value to every point in space, representing quantities like temperature or pressure, while a vector assigns both magnitude and direction to each point, describing quantities such as velocity or force. Fields are typically scalar or tensor quantities defined over a region, whereas vectors specifically express directional attributes as elements of vector spaces. Key differences include the nature of the quantity (scalar vs. directional) and how these quantities vary point-by-point within the spatial domain.
Properties of Fields Explained
Fields are mathematical constructs that assign a single value, such as a scalar or vector, to every point in space, characterized by properties like magnitude and direction for vector fields, or only magnitude for scalar fields. Unlike vectors, which are specific quantities with both magnitude and direction at a single point, fields extend these properties continuously across a region, enabling the representation of physical phenomena like electromagnetic or gravitational forces. Key properties of fields include continuity, differentiability, and the ability to be scalar, vector, or tensorial, defining their behavior and interaction in physics and engineering applications.
Properties of Vectors Explained
Vectors are mathematical entities characterized by both magnitude and direction, distinguishing them from scalar fields that only have magnitude. Key properties of vectors include vector addition, scalar multiplication, and directionality, which allow them to represent physical quantities such as velocity, force, and displacement. Unlike fields that assign values to points in space, vectors maintain consistent algebraic operations that follow specific rules like commutativity and associativity within vector spaces.
Mathematical Operations: Field vs Vector
Fields involve operations like addition, subtraction, multiplication, and division that satisfy closure, associativity, distributivity, and the existence of identity and inverse elements, forming an algebraic structure essential in abstract algebra. Vectors primarily support operations including vector addition, scalar multiplication, and dot or cross products, adhering to linearity and geometric interpretations in vector spaces. Understanding these mathematical operations highlights the foundational difference: fields deal with scalar quantities supporting multiplicative inverses, while vectors represent quantities with both magnitude and direction, governed by linear algebra.
Real-World Examples of Fields
Magnetic fields around the Earth influence compass navigation, guiding travelers by aligning compass needles with the Earth's magnetic vector forces. Temperature distribution across a metal plate, represented as a scalar field, changes continuously without direction, unlike vector fields that include both magnitude and direction like wind velocity on weather maps. Gravitational fields generated by massive bodies such as planets exert forces that can be described as vectors, pointing towards the masses and affecting satellite orbits and tides.
Real-World Applications of Vectors
Vectors are essential in real-world applications such as physics for representing forces, velocity, and acceleration, enabling precise modeling of motion and interaction. In computer graphics, vectors facilitate the manipulation and rendering of images by defining directions and magnitudes for lighting, shading, and transformations. Engineering disciplines rely on vectors to analyze stress, strain, and fluid flow, providing critical insights into structural integrity and system behavior.
Interrelation: Vectors in a Field
Vectors in a field serve as elements that allow both magnitude and direction to be defined within the field's algebraic structure, enabling operations such as vector addition and scalar multiplication. The interrelation between fields and vectors is essential for constructing vector spaces, where scalars from the field scale vectors, preserving linearity and enabling geometric and physical interpretations. This foundational relationship underpins applications in physics, engineering, and mathematics, including solutions to systems of linear equations and transformations in Euclidean spaces.
Common Misconceptions: Field vs Vector
Fields and vectors are often confused, but fields assign a value to every point in space, which can be scalar, vector, or tensor quantities, whereas vectors are specific objects with magnitude and direction. A common misconception is that all fields are vectors; however, scalar fields like temperature distribution and tensor fields like stress also exist. Understanding this distinction is crucial in physics and engineering for correctly interpreting phenomena such as electromagnetic fields and velocity fields in fluid dynamics.
Field Infographic
 libterm.com
libterm.com