Scalar refers to a quantity that has only magnitude and no direction, commonly used in physics and mathematics to describe values such as temperature, mass, or speed. Understanding scalars helps differentiate them from vectors, which have both magnitude and direction, enhancing your grasp of fundamental scientific concepts. Explore the rest of the article to deepen your knowledge of scalar quantities and their applications.
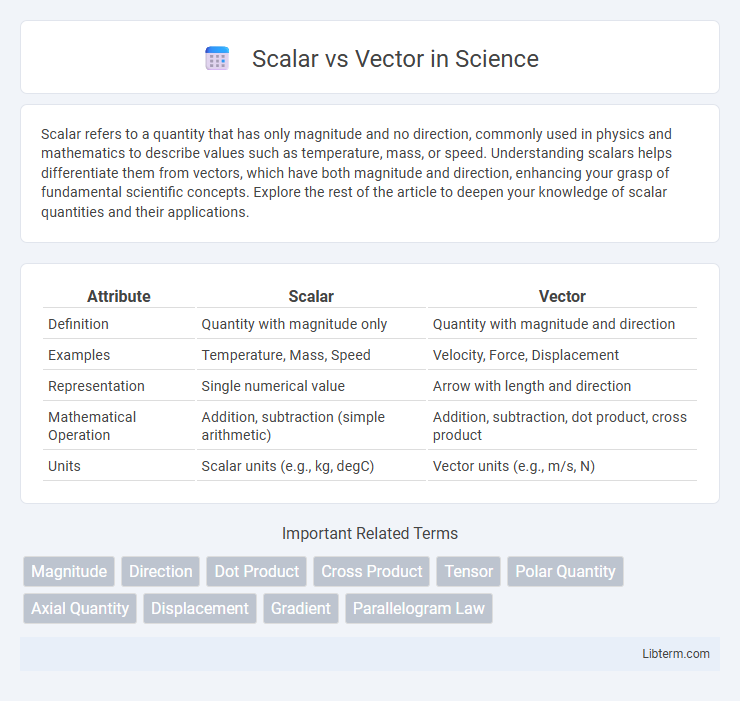
Table of Comparison
| Attribute | Scalar | Vector |
|---|---|---|
| Definition | Quantity with magnitude only | Quantity with magnitude and direction |
| Examples | Temperature, Mass, Speed | Velocity, Force, Displacement |
| Representation | Single numerical value | Arrow with length and direction |
| Mathematical Operation | Addition, subtraction (simple arithmetic) | Addition, subtraction, dot product, cross product |
| Units | Scalar units (e.g., kg, degC) | Vector units (e.g., m/s, N) |
Introduction to Scalars and Vectors
Scalars represent quantities defined solely by magnitude, such as temperature, mass, and time, which have no directional component. Vectors describe quantities possessing both magnitude and direction, exemplified by displacement, velocity, and force. Understanding the distinction between scalars and vectors is fundamental in physics and engineering for accurately analyzing and solving problems involving different physical quantities.
Defining Scalar Quantities
Scalar quantities represent physical properties characterized by magnitude alone, such as temperature, mass, speed, and energy. Unlike vectors, scalars do not possess direction, making them fully described by a single numerical value and appropriate units. Scalar values follow algebraic addition, subtraction, multiplication, and division without the complexity of vector operations.
Understanding Vector Quantities
Vector quantities possess both magnitude and direction, distinguishing them from scalar quantities that only have magnitude. Examples of vector quantities include displacement, velocity, acceleration, and force, each playing a crucial role in physics and engineering. Understanding vectors involves grasping concepts like vector addition, subtraction, and resolution into components, which are essential for accurately describing motion and forces in multidimensional space.
Key Differences Between Scalars and Vectors
Scalars represent quantities with only magnitude, such as temperature, mass, and time, while vectors possess both magnitude and direction, exemplified by velocity, force, and displacement. Scalars are added algebraically, whereas vector addition requires combining both magnitude and direction using methods like the parallelogram rule or component-wise addition. Understanding these distinctions is essential in physics and engineering for accurately describing motion, forces, and other physical phenomena.
Mathematical Representation of Scalars and Vectors
Scalars are mathematically represented as single real numbers, such as temperature (25degC) or mass (5 kg), denoted by variables like \( s \in \mathbb{R} \). Vectors are expressed as ordered tuples or arrays of scalars, for example, \( \mathbf{v} = (v_1, v_2, v_3) \in \mathbb{R}^n \), capturing magnitude and direction in n-dimensional space. Vector notation often uses boldface or arrow symbols, while scalars remain simple numerical values without directional components.
Physical Examples of Scalars
Temperature, mass, and time are classic physical examples of scalars, characterized solely by their magnitude without direction. Unlike vectors such as velocity or force, scalars like energy and speed represent quantities that remain unchanged regardless of the reference frame's orientation. These scalar quantities are fundamental in physics, facilitating straightforward calculations where only size or amount is relevant.
Physical Examples of Vectors
Force, velocity, and displacement are key physical examples of vectors, each characterized by both magnitude and direction. For instance, force applied on an object is vectorial because it has a specific direction along with its magnitude in newtons. Velocity represents the rate of change of displacement and involves directional movement, distinguishing it from scalar quantities such as speed.
Operations Involving Scalars and Vectors
Scalar operations involve basic arithmetic such as addition, subtraction, multiplication, and division of single magnitude values, which lack direction. Vector operations require handling both magnitude and direction, including vector addition, scalar multiplication, dot product, and cross product, essential for calculating angles and projections in physics and engineering. These operations enable accurate modeling of forces, velocities, and other directional quantities in multidimensional spaces.
Importance in Physics and Engineering
Scalars, characterized by magnitude only, simplify calculations in thermodynamics, mass measurement, and energy quantification, providing foundational data essential for system analysis. Vectors, defined by both magnitude and direction, are crucial in mechanics and electromagnetism to represent forces, velocities, and fields, enabling accurate modeling of physical phenomena. Understanding the distinction between scalars and vectors enhances precision in engineering design, structural analysis, and motion prediction.
Conclusion: Choosing Scalar or Vector Quantities
Choosing between scalar and vector quantities depends on the nature of the physical problem. Scalars, defined solely by magnitude, are suitable for measuring simple quantities like temperature, mass, and speed. Vectors, characterized by both magnitude and direction, are essential when describing displacement, velocity, and force to accurately represent motion and interactions.
Scalar Infographic
 libterm.com
libterm.com