A tensor is a mathematical object that generalizes scalars, vectors, and matrices to higher dimensions, playing a crucial role in fields like physics, engineering, and computer science. Tensors enable complex data representation and manipulation, essential for applications such as machine learning, computer vision, and scientific computing. Explore the rest of this article to uncover how understanding tensors can advance your knowledge and practical skills.
Table of Comparison
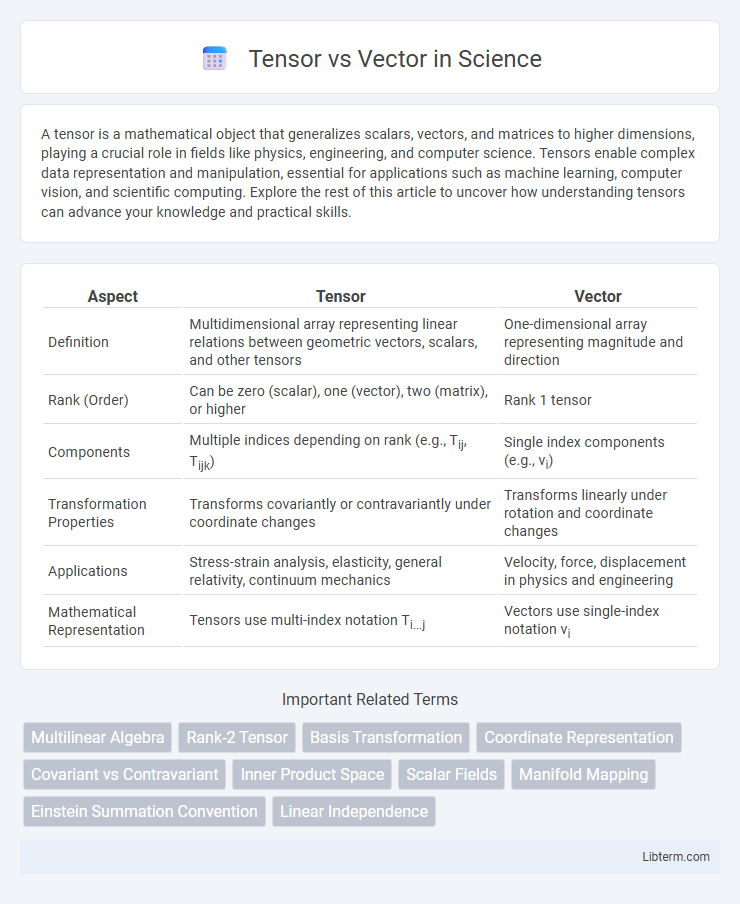
| Aspect | Tensor | Vector |
|---|---|---|
| Definition | Multidimensional array representing linear relations between geometric vectors, scalars, and other tensors | One-dimensional array representing magnitude and direction |
| Rank (Order) | Can be zero (scalar), one (vector), two (matrix), or higher | Rank 1 tensor |
| Components | Multiple indices depending on rank (e.g., Tij, Tijk) | Single index components (e.g., vi) |
| Transformation Properties | Transforms covariantly or contravariantly under coordinate changes | Transforms linearly under rotation and coordinate changes |
| Applications | Stress-strain analysis, elasticity, general relativity, continuum mechanics | Velocity, force, displacement in physics and engineering |
| Mathematical Representation | Tensors use multi-index notation Ti...j | Vectors use single-index notation vi |
Introduction to Tensors and Vectors
Tensors and vectors are fundamental mathematical objects used in physics and engineering to represent quantities with magnitude and direction. A vector is a rank-1 tensor characterized by its components along specific coordinate axes, commonly used to describe velocity or force. Tensors generalize vectors to higher dimensions and ranks, encapsulating more complex relationships such as stress or strain in materials through multi-dimensional arrays.
Defining Vectors: Basic Concepts
Vectors represent quantities with both magnitude and direction, typically defined as ordered arrays of numbers in a coordinate system. They are elements of a vector space and follow operations such as addition and scalar multiplication subject to rules ensuring closure and linearity. Unlike scalars, vectors encode multi-dimensional information crucial for physics, engineering, and computer graphics.
Understanding Tensors: An Overview
Tensors extend the concept of vectors by representing data in multidimensional arrays, enabling the description of more complex relationships in physics and machine learning. Vectors are rank-1 tensors consisting of a single dimension, whereas tensors can have higher ranks, such as matrices (rank-2) or beyond, capturing multidimensional interactions. Understanding tensors involves recognizing their role in encoding geometric and algebraic information across multiple axes, facilitating advanced computations in AI, robotics, and computer vision.
Dimensional Differences: Vector vs Tensor
Vectors are one-dimensional arrays representing magnitude and direction, typically expressed as ordered sets of numbers like coordinates in space. Tensors generalize vectors to higher dimensions, encompassing scalars (zero-dimensional), vectors (one-dimensional), matrices (two-dimensional), and beyond, characterized by their rank or order indicating the number of dimensions. The dimensional difference crucially impacts their applications in physics and machine learning, where tensors capture multi-dimensional data relationships beyond the linear structure of vectors.
Mathematical Representations
Tensors are multi-dimensional arrays that generalize scalars, vectors, and matrices, represented mathematically as elements of a tensor product of vector spaces. Vectors are first-order tensors characterized by a single index and can be expressed as n-dimensional coordinate arrays within a vector space. Unlike vectors, tensors possess multiple indices that allow them to represent higher-dimensional linear relations and transformations.
Real-World Applications
Tensors enable complex data representation in fields like computer vision, where multi-dimensional arrays capture color, depth, and spatial information simultaneously. Vectors serve as foundational elements in machine learning algorithms, representing feature sets and facilitating classification or regression tasks. In physics, tensors describe stress, strain, and electromagnetic fields, while vectors model forces and velocities, highlighting their complementary roles in real-world problem-solving.
Operations Involving Vectors and Tensors
Vector operations include addition, scalar multiplication, and dot products, which transform vectors within a single vector space. Tensor operations extend these concepts through tensor contraction, outer products, and multilinear maps, enabling manipulation of multi-dimensional arrays representing complex relationships in physics and engineering. These operations preserve covariance and contravariance properties critical for consistency in coordinate transformations.
Key Differences: A Comparative Analysis
Tensors generalize vectors by representing multidimensional arrays, allowing data to exist in higher dimensions beyond the one-dimensional structure of vectors. While vectors are specifically rank-1 tensors characterized by magnitude and direction, tensors can have varying ranks, encapsulating complex relationships in fields like physics and machine learning. This dimensional and structural distinction underpins how tensors and vectors are utilized in mathematical modeling and computations.
Importance in Machine Learning and AI
Vectors represent data points as one-dimensional arrays crucial for feature representation in machine learning algorithms. Tensors extend vectors to multidimensional arrays, enabling complex data structures like images, videos, and sequences to be processed efficiently in AI models. Understanding the distinction between tensors and vectors is essential for leveraging deep learning frameworks such as TensorFlow and PyTorch, which rely heavily on tensor operations for computational performance and modeling accuracy.
Conclusion: Choosing Between Tensor and Vector
Choosing between a tensor and a vector depends on the complexity of the data and the dimensionality required for analysis. Vectors represent one-dimensional arrays suited for simple linear data, while tensors extend to multi-dimensional arrays capturing intricate relationships in higher-dimensional spaces. Selecting the appropriate structure hinges on the specific application's need for precision and the ability to model complex phenomena effectively.
Tensor Infographic
 libterm.com
libterm.com