Symbolic logic uses symbols to represent logical expressions, simplifying complex arguments and enhancing clarity in reasoning. It is essential for fields such as mathematics, computer science, and philosophy, providing a structured way to analyze validity and consistency. Explore the rest of the article to deepen your understanding of symbolic logic and its practical applications.
Table of Comparison
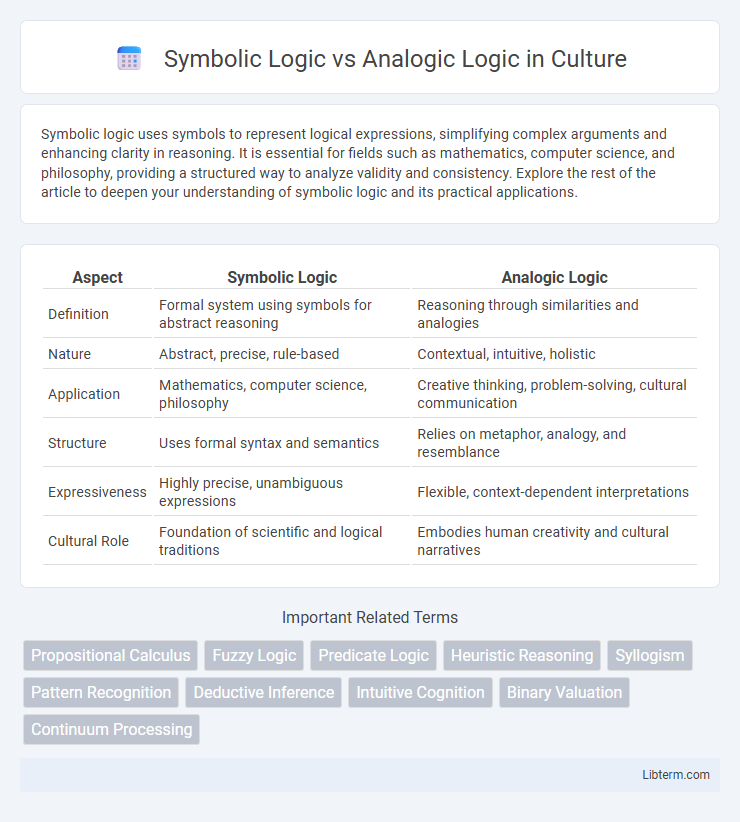
| Aspect | Symbolic Logic | Analogic Logic |
|---|---|---|
| Definition | Formal system using symbols for abstract reasoning | Reasoning through similarities and analogies |
| Nature | Abstract, precise, rule-based | Contextual, intuitive, holistic |
| Application | Mathematics, computer science, philosophy | Creative thinking, problem-solving, cultural communication |
| Structure | Uses formal syntax and semantics | Relies on metaphor, analogy, and resemblance |
| Expressiveness | Highly precise, unambiguous expressions | Flexible, context-dependent interpretations |
| Cultural Role | Foundation of scientific and logical traditions | Embodies human creativity and cultural narratives |
Introduction to Symbolic and Analogic Logic
Symbolic logic uses formal symbols and variables to represent logical expressions, enabling precise and systematic reasoning often seen in mathematics and computer science. Analogic logic relies on the use of analogies, images, and continuous variables to represent and infer relationships, reflecting more intuitive and context-dependent thought processes. Understanding the foundational principles of symbolic and analogic logic clarifies their distinct roles in formal reasoning and human cognition.
Defining Symbolic Logic
Symbolic logic, also known as formal logic, involves the use of symbols and abstract notation to represent logical expressions and relationships, enabling precise manipulation of propositions and arguments. It relies on a structured system of syntax and semantics to analyze validity and inference within mathematical and philosophical contexts. Unlike analogic logic, which emphasizes qualitative and intuitive reasoning based on similarities and analogies, symbolic logic prioritizes exactness and formal proof methods.
Understanding Analogic Logic
Analogic logic operates through the interpretation of relationships and patterns rather than relying on discrete symbols, enabling a more intuitive and context-sensitive understanding of information. Unlike symbolic logic, which uses formal symbols and strict rules to represent propositions and infer conclusions, analogic logic mimics human cognitive processes by emphasizing similarity, metaphor, and analogy. This approach is especially effective in fields such as artificial intelligence and cognitive science, where modeling natural thought patterns and problem-solving techniques requires nuanced context recognition.
Historical Evolution of Logical Systems
Symbolic logic, emerging prominently in the 19th century with pioneers like George Boole and Gottlob Frege, transformed traditional reasoning by formalizing logic through algebraic symbols and precise syntax. Analogic logic, rooted in Aristotelian and early philosophical traditions, relied on diagrammatic and analogy-based reasoning to represent relationships and infer conclusions. The historical evolution reflects a shift from intuitive, visual methods to rigorous, symbolic systems underlining modern computational logic and formal proof techniques.
Core Principles: Symbolic vs. Analogic Reasoning
Symbolic logic relies on abstract symbols and formal rules to represent and manipulate logical statements, enabling precise deduction and computation. Analogic logic, in contrast, emphasizes reasoning through similarity, patterns, and analogies, facilitating intuitive understanding and problem-solving in ambiguous contexts. Core principles of symbolic reasoning include syntactic manipulation and truth-functional evaluation, whereas analogic reasoning centers on mapping relationships and structural correspondences between different domains.
Applications in Mathematics and Science
Symbolic logic provides a formal language for representing mathematical proofs and algorithms, enabling precise manipulation of abstract concepts within fields like computer science and advanced mathematics. Analogic logic facilitates reasoning through patterns and similarities, playing a crucial role in scientific modeling, hypothesis formation, and qualitative analysis. Together, these logics enhance problem-solving by combining exact symbolic computations with intuitive analogical reasoning in scientific discovery and mathematical innovation.
Real-World Scenarios: Practical Usage of Each Logic
Symbolic logic excels in real-world scenarios requiring precise mathematical reasoning, such as computer programming, formal verification, and artificial intelligence, where clear, unambiguous rules govern system behavior. Analogic logic proves more practical in everyday decision-making and problem-solving situations involving pattern recognition, creative thinking, and interpreting ambiguous data, such as diagnosing medical conditions or making strategic business choices. Understanding the application context determines whether symbolic or analogic logic optimally supports effective reasoning and practical outcomes.
Cognitive Impact: Human Thinking and Logic
Symbolic logic enhances human cognitive capacity by enabling abstract reasoning through the manipulation of symbols and formal rules, facilitating clear and precise problem-solving. Analogic logic relies on patterns and similarity-based reasoning, which supports intuitive thinking and creative insight but may lack the precision of symbolic systems. Together, these logical frameworks shape diverse cognitive strategies, influencing how individuals process information and approach complex problems.
Advantages and Limitations of Both Approaches
Symbolic logic excels in precision and formal reasoning, enabling clear manipulation of abstract symbols for deductive proofs but often lacks intuitive understanding of real-world scenarios. Analogic logic offers intuitive problem-solving through pattern recognition and analogies, facilitating creative insights but may suffer from vagueness and difficulty in formal validation. Balancing symbolic logic's rigor with analogic logic's flexibility provides a comprehensive framework for diverse cognitive and computational tasks.
Future Trends: Integration and Technological Implications
Symbolic logic, with its precision in formal reasoning, is increasingly integrated with analogic logic's capacity for pattern recognition to advance artificial intelligence and machine learning technologies. Future trends indicate a convergence where symbolic frameworks enhance the interpretability of analogic systems, enabling more robust decision-making in autonomous systems and natural language processing. This integration drives developments in quantum computing and cognitive architectures, positioning combined logical paradigms at the forefront of technological innovation.
Symbolic Logic Infographic
 libterm.com
libterm.com