The gradient method is a powerful optimization technique used to find the minimum or maximum of a function by iteratively moving in the direction of the steepest descent or ascent. It is widely applied in machine learning, data science, and engineering to solve complex problems efficiently. Discover how mastering the gradient method can transform your approach by exploring the rest of this article.
Table of Comparison
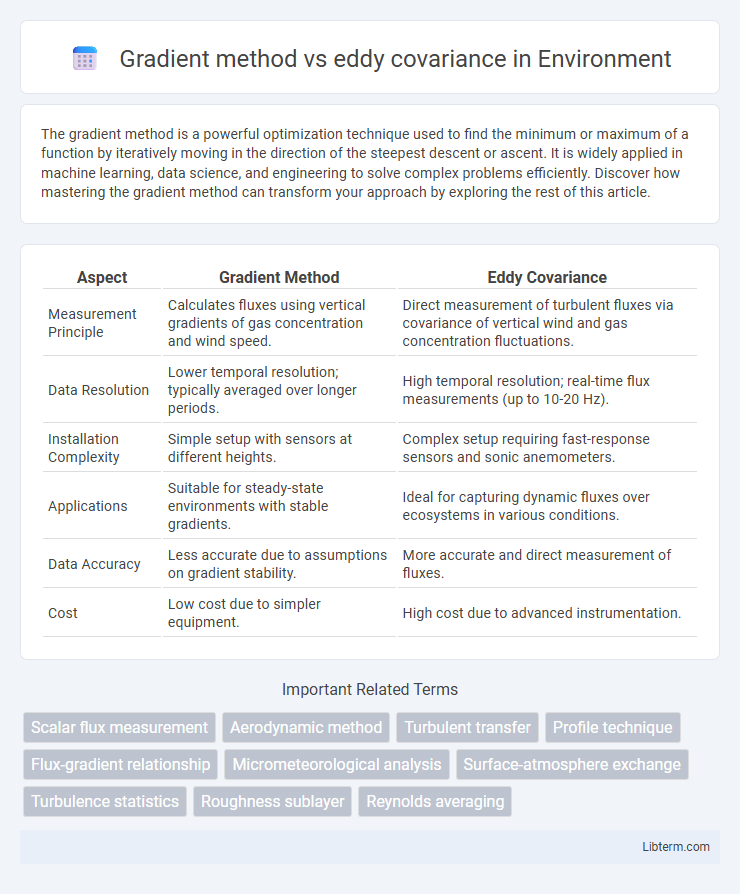
| Aspect | Gradient Method | Eddy Covariance |
|---|---|---|
| Measurement Principle | Calculates fluxes using vertical gradients of gas concentration and wind speed. | Direct measurement of turbulent fluxes via covariance of vertical wind and gas concentration fluctuations. |
| Data Resolution | Lower temporal resolution; typically averaged over longer periods. | High temporal resolution; real-time flux measurements (up to 10-20 Hz). |
| Installation Complexity | Simple setup with sensors at different heights. | Complex setup requiring fast-response sensors and sonic anemometers. |
| Applications | Suitable for steady-state environments with stable gradients. | Ideal for capturing dynamic fluxes over ecosystems in various conditions. |
| Data Accuracy | Less accurate due to assumptions on gradient stability. | More accurate and direct measurement of fluxes. |
| Cost | Low cost due to simpler equipment. | High cost due to advanced instrumentation. |
Introduction to Gradient Method and Eddy Covariance
The Gradient Method estimates gas fluxes by measuring vertical concentration gradients and applying Fick's law of diffusion, primarily used in soil or canopy studies for gas exchange quantification. Eddy Covariance directly measures turbulent fluxes of gases by analyzing high-frequency wind velocity and scalar concentration fluctuations, providing real-time ecosystem-atmosphere exchange data. Both methods are essential in micrometeorology, with the Gradient Method offering simpler, cost-effective measurements and Eddy Covariance delivering more precise and continuous flux observations.
Principles of the Gradient Method
The Gradient Method estimates gas fluxes by measuring vertical concentration gradients between two or more heights and applying Fick's Law of diffusion, assuming steady-state conditions and negligible advection. This technique relies on precise measurements of scalar concentration differences and turbulent diffusivity coefficients to calculate fluxes. Compared to eddy covariance, the Gradient Method requires less complex instrumentation but provides lower temporal resolution and can be influenced by atmospheric stability variations.
Fundamentals of Eddy Covariance Technique
The eddy covariance technique measures turbulent fluxes of gases between the surface and atmosphere by directly capturing rapid fluctuations in vertical wind velocity and scalar concentrations, ensuring high temporal resolution data critical for accurate ecosystem gas exchange estimates. Unlike the gradient method, which infers fluxes indirectly through concentration gradients and turbulent diffusion coefficients, eddy covariance provides direct, continuous flux measurements without relying on empirical assumptions about turbulence. This method's fundamental components include a three-dimensional sonic anemometer and fast-response gas analyzers, enabling precise quantification of net exchanges of CO2, water vapor, and energy essential for understanding ecosystem functioning and climate interactions.
Key Differences in Measurement Approaches
The Gradient method estimates gas fluxes by measuring vertical concentration gradients and applying Fick's law of diffusion, relying on steady-state assumptions and stable atmospheric conditions. Eddy Covariance directly measures turbulent fluxes by correlating high-frequency fluctuations of vertical wind speed and scalar concentrations, capturing instantaneous exchanges without requiring simplified dispersion models. This fundamental difference makes Eddy Covariance more accurate for dynamic environments, while the Gradient method is simpler but less precise under variable turbulence.
Applications in Ecosystem Gas Exchange Studies
The Gradient method and Eddy Covariance technique both serve crucial roles in quantifying ecosystem gas exchange, particularly carbon dioxide and water vapor fluxes. Gradient methods, relying on concentration differences over a vertical profile, are often employed in forest understory or complex terrain where Eddy Covariance towers are less feasible. Eddy Covariance, providing high-frequency, direct flux measurements, is preferred in open-canopy ecosystems like grasslands and agricultural fields due to its accuracy in capturing turbulent gas exchange dynamics.
Instrumentation and Data Requirements
The Gradient method utilizes vertical profiles of wind speed and scalar concentrations measured by fast-response sensors mounted at multiple heights to estimate fluxes through gradient calculations, requiring precise calibration and stable atmospheric conditions. Eddy Covariance relies on high-frequency (10-20 Hz) measurements from 3D sonic anemometers and gas analyzers at a single height to directly capture turbulent fluxes, demanding costly and sophisticated instrumentation with rigorous data processing to correct for sensor separation and coordinate rotation. Data requirements for the Gradient method include multiple spatially separated sampling points and steady-state atmospheric assumptions, whereas Eddy Covariance mandates high temporal resolution data and extensive post-processing to address sensor drift, flux stationarity, and footprint variability.
Advantages and Limitations of Each Method
The Gradient method offers simplicity and cost-effectiveness by measuring vertical concentration differences to estimate fluxes but is limited by assumptions of steady-state conditions and homogeneity in the measurement area. Eddy covariance provides direct, high-frequency flux measurements with fine temporal resolution, making it highly accurate for turbulent environments but requires expensive, complex instrumentation and extensive data processing. Both methods are complementary; gradient method suits simpler studies with budget constraints, while eddy covariance is preferred for detailed, dynamic ecosystem flux analyses.
Accuracy, Precision, and Sources of Error
The Gradient method offers moderate accuracy in estimating gas fluxes but is often limited by lower spatial resolution and sensitivity to turbulence variability, impacting its precision. Eddy Covariance provides higher accuracy and precision by directly measuring turbulent fluxes with fast-response sensors, capturing rapid fluctuations in gas exchange. Sources of error for the Gradient method include assumptions about steady-state conditions and imperfect sensor placement, whereas Eddy Covariance errors stem mainly from sensor calibration, flux footprint heterogeneity, and data gap-filling techniques.
Suitability for Different Environmental Conditions
The gradient method suits stable, low-turbulence environments where vertical gradients of scalar properties like temperature or gas concentration are well-defined, such as forests with uniform canopy structure. Eddy covariance excels in diverse and dynamic environments, capturing rapid fluctuations in vertical wind and scalar quantities, making it ideal for heterogeneous landscapes and varying atmospheric conditions. While the gradient method may underestimate fluxes during turbulent or variable conditions, eddy covariance provides high-frequency, precise measurements crucial for assessing ecosystem exchanges accurately.
Future Trends and Technological Advancements
Emerging trends in micrometeorological measurements highlight the integration of real-time data analytics and machine learning algorithms with both gradient method and eddy covariance systems to enhance accuracy and temporal resolution. Advanced sensor technologies and miniaturized, low-power devices are enabling wider deployment across diverse ecosystems, facilitating continuous monitoring of gas exchange and turbulence. Future developments are expected to focus on sensor fusion, combining gradient and eddy covariance data streams to improve spatial representativeness and reduce uncertainties in flux estimations.
Gradient method Infographic
 libterm.com
libterm.com