Conic sections are curves obtained by intersecting a plane with a double-napped cone, including ellipses, parabolas, and hyperbolas, each with unique mathematical properties and real-world applications. Understanding conic sections is essential in fields such as astronomy, engineering, and physics, where they describe orbital paths, reflectors, and projectile trajectories. Discover how mastering conic sections can enhance your problem-solving skills and explore the detailed properties in the rest of this article.
Table of Comparison
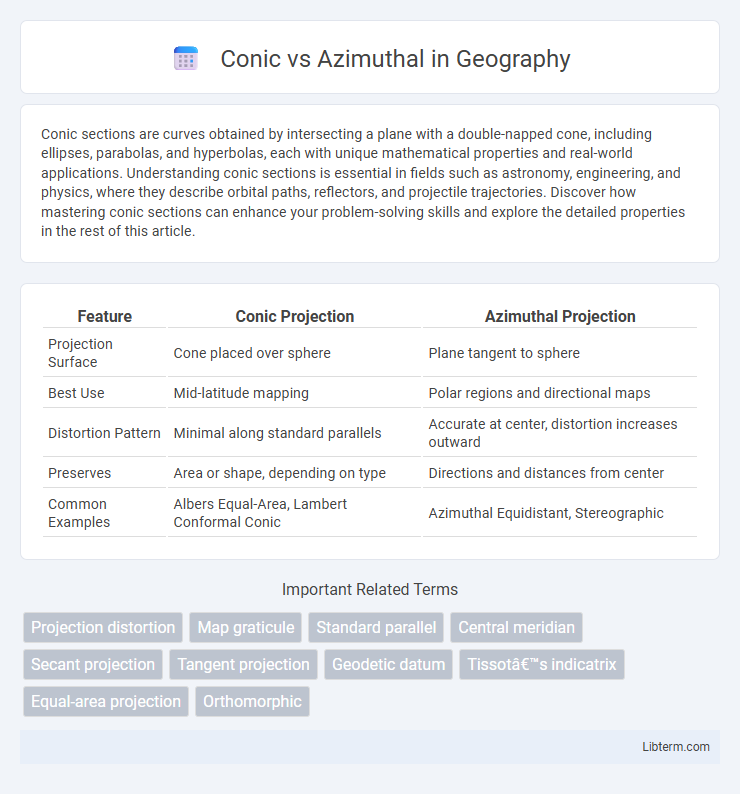
| Feature | Conic Projection | Azimuthal Projection |
|---|---|---|
| Projection Surface | Cone placed over sphere | Plane tangent to sphere |
| Best Use | Mid-latitude mapping | Polar regions and directional maps |
| Distortion Pattern | Minimal along standard parallels | Accurate at center, distortion increases outward |
| Preserves | Area or shape, depending on type | Directions and distances from center |
| Common Examples | Albers Equal-Area, Lambert Conformal Conic | Azimuthal Equidistant, Stereographic |
Introduction to Conic and Azimuthal Map Projections
Conic map projections represent the Earth on a cone placed over the globe, typically used for mid-latitude regions due to their balanced distortion along standard parallels. Azimuthal map projections project the globe onto a plane, maintaining accurate directions from a central point, making them ideal for polar regions and navigation purposes. Both projection types serve specific geographic needs by minimizing distortion in targeted areas.
Defining Conic Map Projections
Conic map projections are defined by projecting the globe onto a cone placed over a portion of the Earth, typically along one or two standard parallels, which reduces distortion in mid-latitude regions. These projections are ideal for representing countries or continents with an east-west orientation, offering a balance between shape and area accuracy. Unlike azimuthal projections that project onto a plane from a single point, conic projections provide consistent scale along the standard parallels and are widely used for regional and topographic maps.
Understanding Azimuthal Map Projections
Azimuthal map projections represent the Earth on a flat plane, projecting points from the globe onto a tangent or secant plane, often centered on a specific point such as the poles or the equator. These projections preserve directions and distances from the center point, making them valuable for applications in aviation, radio communication, and polar region mapping. Unlike conic projections that wrap the Earth in a cone, azimuthal projections provide accurate angular relationships and are preferred for azimuth and distance measurements from a central location.
Key Differences Between Conic and Azimuthal Projections
Conic projections use a cone-shaped surface to project the Earth's features, producing minimal distortion along specific latitude parallels, making them ideal for mapping mid-latitude regions. Azimuthal projections project the Earth onto a flat plane tangential to a single point, preserving accurate directions from the center point but causing distortion that increases outward. Key differences include conic projections maintaining scale along standard parallels while azimuthal projections preserve true direction and distance from the center point.
Advantages of Conic Map Projections
Conic map projections provide superior accuracy for mapping mid-latitude regions due to their ability to minimize distortion along standard parallels, making them ideal for countries and continents extending predominantly east-west. These projections maintain shape and area balance better than azimuthal projections over large areas, which is essential for regional planning and navigation. Furthermore, conic projections offer scalable flexibility, allowing cartographers to adjust cone angles and standard parallels to optimize accuracy for specific geographic extents.
Benefits of Azimuthal Map Projections
Azimuthal map projections offer precise distance and direction measurements from a central point, making them ideal for navigational and meteorological applications. These projections preserve angles and true directions, enhancing accuracy for radio and air route planning. Unlike conic projections, azimuthal maps provide an undistorted view of polar regions, supporting scientific research and satellite imagery analysis.
Limitations of Conic Projections
Conic projections, such as Albers and Lambert, are limited by distortion that increases away from the standard parallels, causing inaccuracies in scale and shape especially near the poles. These projections are less suitable for mapping polar regions or global datasets due to their inability to represent the entire Earth without significant distortion. In contrast, azimuthal projections maintain accurate direction from a central point, making them preferable for polar maps and applications requiring true azimuthal properties.
Drawbacks of Azimuthal Map Projections
Azimuthal map projections distort area and shape increasingly as one moves away from the central point, leading to significant inaccuracies in representing large regions or entire continents. These projections are limited in their ability to preserve scale and direction outside the central point, which restricts their usefulness for global navigation and spatial analysis. Compared to Conic projections, which better balance distortion across mid-latitude areas, Azimuthal projections struggle with maintaining proportional distances and true compass bearings across wider geographic extents.
Common Use Cases for Each Projection Type
Conic projections are commonly used for mapping mid-latitude regions with an east-west orientation, such as the United States, Europe, and Russia, due to their ability to balance distortion along parallels. Azimuthal projections excel in representing polar areas and for applications requiring accurate direction or distance from a central point, such as air route mapping and seismic studies. Both projection types serve specific geographic purposes, with conic suited for regional mapping and azimuthal optimal for focused, directional analysis.
Choosing the Right Projection: Conic or Azimuthal?
Selecting between conic and azimuthal projections depends on the map's intended use and geographic coverage. Conic projections are optimal for mid-latitude regions with east-west orientation, offering balanced distortion and accurate area representation. Azimuthal projections excel in mapping polar areas or focusing on specific points, preserving direction and distances from the center.
Conic Infographic
 libterm.com
libterm.com