The geoid represents Earth's mean sea level extended through the continents, serving as a crucial reference surface for measuring precise elevations. Understanding the geoid helps improve accuracy in satellite navigation, geodesy, and oceanography by accounting for variations in Earth's gravitational field. Discover how this complex model impacts Your daily navigation and scientific measurements in the rest of the article.
Table of Comparison
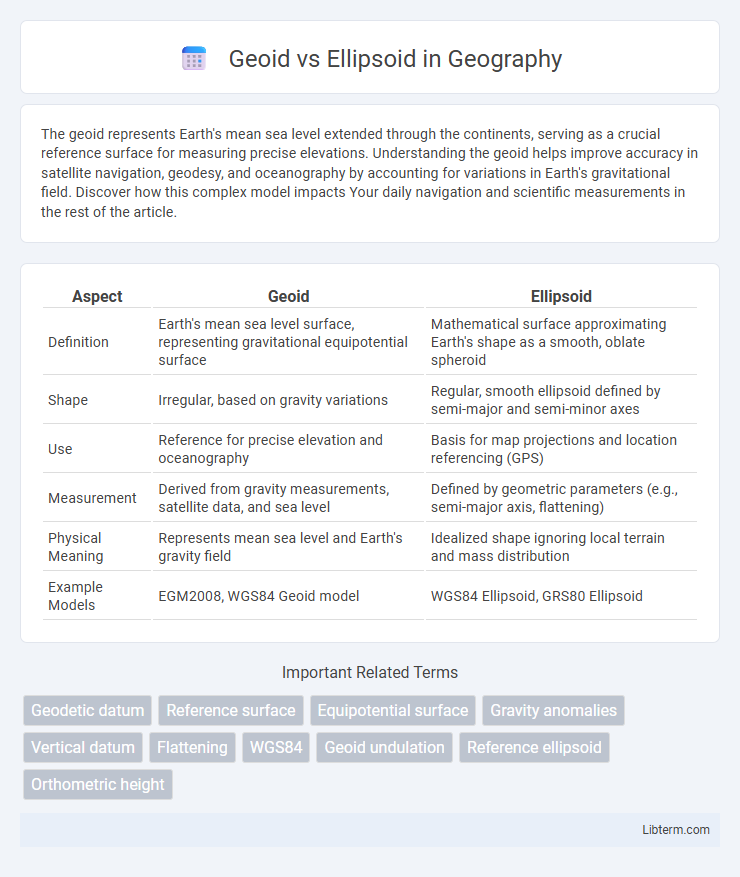
| Aspect | Geoid | Ellipsoid |
|---|---|---|
| Definition | Earth's mean sea level surface, representing gravitational equipotential surface | Mathematical surface approximating Earth's shape as a smooth, oblate spheroid |
| Shape | Irregular, based on gravity variations | Regular, smooth ellipsoid defined by semi-major and semi-minor axes |
| Use | Reference for precise elevation and oceanography | Basis for map projections and location referencing (GPS) |
| Measurement | Derived from gravity measurements, satellite data, and sea level | Defined by geometric parameters (e.g., semi-major axis, flattening) |
| Physical Meaning | Represents mean sea level and Earth's gravity field | Idealized shape ignoring local terrain and mass distribution |
| Example Models | EGM2008, WGS84 Geoid model | WGS84 Ellipsoid, GRS80 Ellipsoid |
Introduction to Geoid and Ellipsoid
The geoid represents the Earth's mean sea level adjusted for gravitational variations, providing an irregular but physically meaningful surface used in precise elevation measurements. The ellipsoid, a mathematically defined smooth surface formed by rotating an ellipse, serves as a simplified reference model for geodetic calculations and mapping. Understanding the differences between the geoid and ellipsoid is essential for accurate positioning, surveying, and navigation in geodesy.
Defining the Geoid
The geoid is the equipotential surface of Earth's gravity field that best fits mean sea level globally, serving as a reference for measuring precise elevations. Unlike the mathematical ellipsoid, which is a smooth and regular shape approximating Earth's size and shape, the geoid accounts for variations in gravitational acceleration caused by Earth's uneven mass distribution. This makes the geoid essential for accurate geodetic and oceanographic measurements, as it reflects true gravitational potential rather than an idealized geometric surface.
Defining the Ellipsoid
The ellipsoid is a mathematically defined surface that approximates the shape of the Earth by smoothing out irregularities found in the geoid. It is generated by rotating an ellipse around its minor axis, creating a smooth, regular shape characterized by parameters such as the semi-major axis and flattening factor. This simplified geometric model enables precise calculations in geodesy, satellite navigation, and mapping systems by serving as a reference datum for coordinate measurements.
Key Differences between Geoid and Ellipsoid
The geoid represents the Earth's mean sea level adjusted for gravitational variations, reflecting the true physical shape of the planet, while the ellipsoid is a mathematically defined smooth surface approximating the Earth's shape for mapping and navigation. Key differences include the geoid's irregular, undulating form influenced by gravitational anomalies, compared to the ellipsoid's regular, oblate spheroid shape based on averaged measurements. Geoid heights vary relative to the ellipsoid and are crucial for accurate elevation and satellite positioning systems like GPS.
Importance in Geodesy and Mapping
The geoid represents the Earth's mean sea level and serves as a crucial reference for measuring precise elevations in geodesy, reflecting gravitational variations across the planet's surface. The ellipsoid provides a mathematically simplified, smooth surface used for coordinate systems and satellite positioning, enabling consistent global mapping and navigation. Combining geoid undulations with ellipsoid models ensures accurate topographic and geospatial data essential for surveying, engineering, and land management applications.
Measurement Methods and Techniques
Measurement methods for the geoid involve satellite gravimetry and terrestrial gravimetric surveys that capture variations in Earth's gravitational field, enabling precise modeling of the geoid's irregular surface. Ellipsoid measurements rely on geodetic GPS and satellite positioning systems that assume a smooth, mathematically defined surface based on Earth's rotation and shape parameters. Techniques such as satellite altimetry complement gravimetric data to refine geoid models, while ellipsoid determination uses reference frames like WGS84 for consistent spatial positioning.
Applications in GPS and Navigation
The geoid represents Earth's mean sea level, providing a true physical reference for elevation measurements, essential in precise GPS altitude determinations and surveying tasks. The ellipsoid offers a mathematically simplified, smooth surface used as a baseline for GPS satellite positioning and global navigation systems, enabling rapid and consistent coordinate calculations. Combining geoid and ellipsoid models enhances navigation accuracy by correcting GPS height data to reflect true orthometric heights critical for aviation, maritime, and land-based positioning applications.
Advantages and Limitations of Each Model
The geoid provides a more accurate representation of Earth's true shape by reflecting variations in gravitational forces, making it essential for precise elevation and sea level measurements. However, its irregular shape and complex calculations limit its practical use in global mapping and navigation systems. The ellipsoid offers a mathematically simple model ideal for GPS and cartography due to its smooth, regular shape, but it cannot account for local gravitational anomalies, reducing its accuracy in geophysical and oceanographic applications.
Real-World Examples and Case Studies
The geoid represents Earth's true mean sea level, crucial for precise sea-level measurements in coastal engineering projects, such as the Dutch Delta Works, where flood defenses rely on accurate tidal data. In contrast, ellipsoids provide mathematical models for global positioning systems like GPS, exemplified by WGS84, which underpins navigation accuracy worldwide, including aviation and maritime applications. Case studies from geophysical surveys in the Himalayas use geoid height anomalies to assess tectonic activity, highlighting the geoid's role in earthquake risk assessment compared to the ellipsoid's stability as a reference surface.
Conclusion: Choosing the Right Reference Surface
Selecting the appropriate reference surface depends on the application's precision requirements and geographical extent; the geoid models Earth's gravitational field and sea level variations, offering higher accuracy for elevations and geophysical studies. The ellipsoid provides a mathematically simple, smooth surface ideal for GPS positioning and mapping over large areas, ensuring computational efficiency. Combining the geoid and ellipsoid enables enhanced accuracy in surveying, navigation, and geodesy by correcting ellipsoidal heights to orthometric heights.
Geoid Infographic
 libterm.com
libterm.com