The disjunctive property in mathematics states that if a product of two elements is zero, then at least one of the elements must be zero. This principle is fundamental in solving equations and is applied extensively in algebraic problem-solving scenarios. Explore the rest of the article to understand how this property can simplify your approach to complex equations.
Table of Comparison
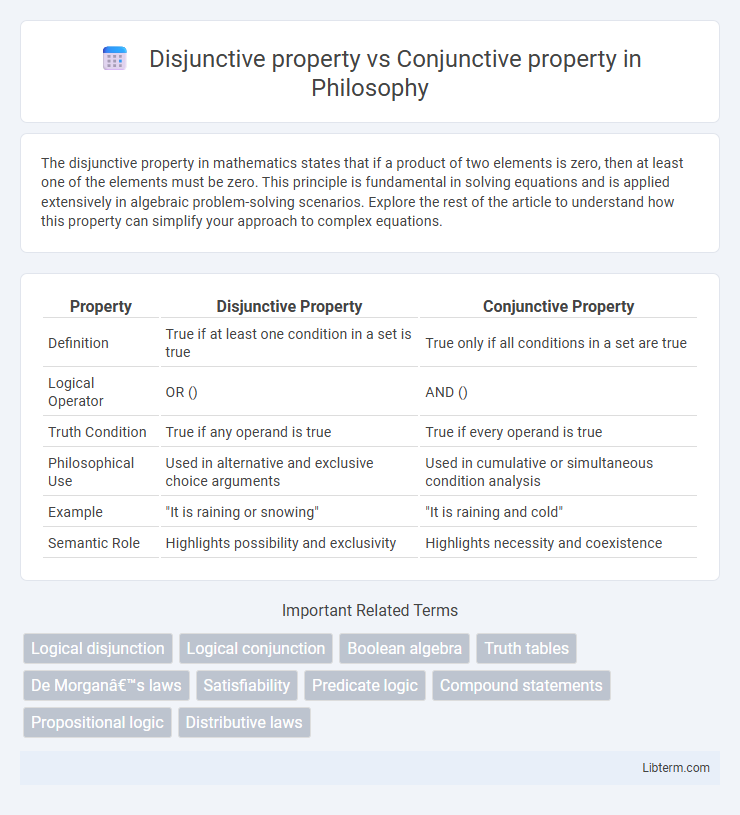
| Property | Disjunctive Property | Conjunctive Property |
|---|---|---|
| Definition | True if at least one condition in a set is true | True only if all conditions in a set are true |
| Logical Operator | OR () | AND () |
| Truth Condition | True if any operand is true | True if every operand is true |
| Philosophical Use | Used in alternative and exclusive choice arguments | Used in cumulative or simultaneous condition analysis |
| Example | "It is raining or snowing" | "It is raining and cold" |
| Semantic Role | Highlights possibility and exclusivity | Highlights necessity and coexistence |
Introduction to Disjunctive and Conjunctive Properties
Disjunctive property refers to a condition where at least one of multiple criteria must be satisfied, emphasizing alternative possibilities within a logical or mathematical framework. Conjunctive property requires that all specified conditions be met simultaneously, highlighting the necessity of combined criteria for validity. Understanding these properties is crucial for logic, database queries, and rule-based systems, as they dictate how information is processed and filtered.
Definition of Disjunctive Property
The disjunctive property refers to a situation where at least one of several propositions is true, represented by the logical operator "or" (), meaning the truth of any single component validates the entire statement. In contrast, the conjunctive property requires all propositions to be true simultaneously, linked by the "and" () operator, to make the overall statement true. Understanding the disjunctive property is essential in logic, mathematics, and computer science for evaluating alternative conditions or possibilities.
Definition of Conjunctive Property
The conjunctive property in mathematics and logic refers to a condition where multiple statements or conditions must all be true simultaneously for the entire statement to hold true. This property is essential in fields like set theory, probability, and programming, where combining criteria with "and" (logical conjunction) defines the overall validity of a condition. Understanding the conjunctive property enables precise formulation and analysis of compound statements, ensuring all components satisfy specified requirements.
Key Differences Between Disjunctive and Conjunctive Properties
Disjunctive properties characterize entities that can have one among multiple distinct values, where only one property is applicable at a time, such as a person being either a student or a teacher. Conjunctive properties require all specified conditions or attributes to be simultaneously true, representing a combination of features that must coexist, like a person being a student and a member of a sports club. The key difference lies in that disjunctive properties denote exclusive alternatives, while conjunctive properties represent the intersection of multiple criteria.
Logical Representation and Notation
The disjunctive property in logical representation is characterized by the use of the logical OR operator ( ), denoting that at least one of multiple propositions must be true, typically expressed as A B. The conjunctive property employs the logical AND operator ( ), signifying that all combined propositions must be true simultaneously, represented as A B. In formal notation, disjunction allows for alternative truth values among components, while conjunction requires the co-truth of every constituent to satisfy the overall statement.
Real-World Examples of Disjunctive Property
The disjunctive property in mathematics allows an equation or inequality to be true if at least one of the multiple conditions is satisfied, exemplified in real-world scenarios such as qualifying criteria for job applications where a candidate must have either a degree or relevant experience. In contrast, the conjunctive property requires all conditions to be met simultaneously, similar to safety regulations demanding that a machine must be equipped with both a guard and an emergency stop button to operate legally. Understanding these properties aids in designing logical conditions in programming, decision-making, and legal frameworks where either inclusive or exclusive conditions apply.
Real-World Examples of Conjunctive Property
The conjunctive property in mathematics states that the product of two numbers equals zero if and only if at least one of the numbers is zero, exemplified in real-world scenarios such as quality control where a product fails inspection if at least one defect exists. In manufacturing, the conjunctive property helps identify failure conditions by testing multiple components together, ensuring that zero defects yield a functional product. This contrasts with the disjunctive property, which deals with logical separation rather than the multiplicative zero condition essential in systems reliability analysis.
Applications in Mathematics and Logic
The disjunctive property in mathematics and logic allows a system to infer that if a disjunction (A or B) holds, then at least one of its components must hold, which is crucial in proof theory and non-classical logics like intuitionistic logic. The conjunctive property states that a proof of a conjunction (A and B) requires proofs of both components individually, underlying the structure of constructive proofs and the foundations of type theory. Applications in automated theorem proving, type systems in programming languages, and formal verification rely heavily on these properties to manage logical inference and computational interpretation of proofs.
Common Mistakes and Misconceptions
Confusing disjunctive and conjunctive properties often leads to misapplying logical operators, such as interpreting "or" (disjunctive) as exclusive instead of inclusive. A common mistake is assuming conjunctive property requires only one condition to be true, whereas it actually demands all conditions to be satisfied simultaneously. Overlooking these distinctions can cause errors in mathematical proofs, programming logic, and formal reasoning tasks.
Conclusion: Importance of Understanding Both Properties
Understanding both disjunctive and conjunctive properties is essential for accurate analysis in database theory and logic. The disjunctive property involves conditions where at least one must be true, enhancing flexibility in query design, while the conjunctive property demands all conditions be met, ensuring precise filtering. Mastery of these properties improves decision-making, optimizes search algorithms, and strengthens data integrity across computational applications.
Disjunctive property Infographic
 libterm.com
libterm.com