A universal property defines objects up to a unique isomorphism based on their relationships with other objects in a category, capturing their essence in a concise and abstract manner. In mathematics, it serves as a foundational concept for constructing and understanding objects through morphisms and commutative diagrams. Explore the rest of the article to deepen your understanding of how universal properties unify diverse structures across various fields.
Table of Comparison
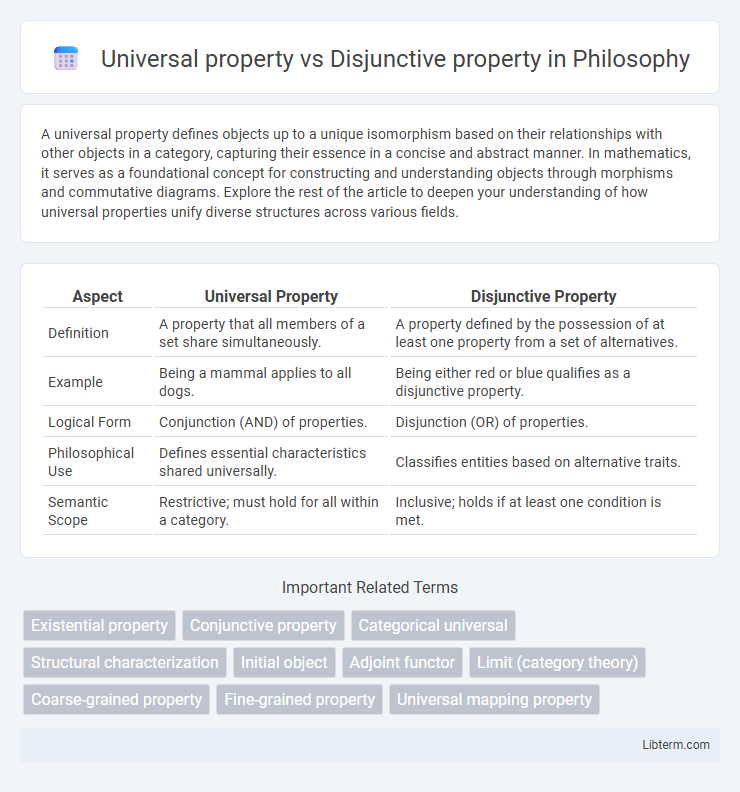
| Aspect | Universal Property | Disjunctive Property |
|---|---|---|
| Definition | A property that all members of a set share simultaneously. | A property defined by the possession of at least one property from a set of alternatives. |
| Example | Being a mammal applies to all dogs. | Being either red or blue qualifies as a disjunctive property. |
| Logical Form | Conjunction (AND) of properties. | Disjunction (OR) of properties. |
| Philosophical Use | Defines essential characteristics shared universally. | Classifies entities based on alternative traits. |
| Semantic Scope | Restrictive; must hold for all within a category. | Inclusive; holds if at least one condition is met. |
Introduction to Universal and Disjunctive Properties
Universal properties characterize objects by specifying a unique morphism that factors through any given construction, serving as foundational tools in category theory to define limits and colimits. Disjunctive properties involve conditions where an object satisfies at least one among several alternatives, often used to analyze coproducts and sum types. Understanding these properties is crucial for encapsulating abstract mathematical structures and enabling precise reasoning in algebra, topology, and theoretical computer science.
Defining Universal Property
The Universal property defines a concept where a unique morphism exists from any object to a given object that satisfies certain conditions, ensuring a form of optimal or canonical mapping in category theory. It captures the essence of objects characterized by their relationships through unique factorization, such as products, coproducts, limits, and colimits. Unlike the Disjunctive property, which emphasizes exclusive or separate conditions, the Universal property guarantees existence and uniqueness of morphisms that preserve structure universally across the category.
Defining Disjunctive Property
A Disjunctive Property in mathematics and logic is characterized by the ability to satisfy at least one condition from a set of alternatives, contrasting with a Universal Property that requires satisfying all conditions simultaneously. It involves properties that hold true through a logical OR relationship among the components, often used to express flexibility or alternative scenarios in theory and category theory. Defining a Disjunctive Property emphasizes the existence of multiple distinct paths or objects where one or more fulfill the property, enabling decompositions and case-based reasoning.
Key Differences Between Universal and Disjunctive Properties
Universal properties apply to all elements within a set, ensuring that every member satisfies a given condition, whereas disjunctive properties indicate that at least one element in the set satisfies one of several possible conditions. The universal property enforces a comprehensive rule across the entire collection, while the disjunctive property allows for flexibility by requiring just one condition to hold true among alternatives. This fundamental distinction affects logical structures, as universal properties are expressed through conjunctions, and disjunctive properties are represented by disjunctions in formal logic.
Theoretical Foundations and Logical Implications
Universal property provides a foundational concept in category theory that characterizes objects uniquely up to isomorphism by their relationships through morphisms, ensuring a universal mapping property that preserves structure consistently. Disjunctive property, often used in logic and set theory, involves the principle where a property holds if at least one of several distinct conditions or sets is satisfied, reflecting an inclusive or alternative condition. The logical implications of universal property support the construction of limits, colimits, and adjoint functors, while disjunctive properties influence decision procedures and branching in logical proofs and model theory.
Applications in Mathematics and Logic
Universal properties characterize objects by their unique mapping relationships in category theory, essential for defining concepts like products and limits. Disjunctive properties, often used in logic and set theory, describe elements satisfying at least one condition within a union, crucial in proof theory and decision-making processes. Applications in mathematics exploit universal properties to construct canonical objects, while logic uses disjunctive properties to analyze compound statements and optimize algorithms in automated reasoning.
Universal Property in Category Theory
The Universal Property in Category Theory characterizes an object by its unique factorization or mapping property relative to other objects, often described through initial or terminal objects, limits, or colimits. It provides an abstract and highly general framework to define constructions like products, coproducts, and pullbacks by specifying universal morphisms. Unlike the Disjunctive Property, which deals more with logical combinations of properties, the Universal Property emphasizes uniqueness and universality of morphisms in categorical diagrams.
Disjunctive Property in Set Theory and Logic
The Disjunctive Property in set theory and logic highlights that for any element belonging to a union of sets, the element must belong to at least one of those sets, aligning with the inclusive "or" operation in propositional logic. This property contrasts with the Universal Property, which concerns elements belonging to all sets in a given collection, reflecting the logical "and" operation. Understanding the Disjunctive Property is essential for reasoning about membership and subsets in unions, providing foundational insight into how elements distribute across combined sets.
Semantic Importance in Computational Contexts
Universal property ensures a condition holds for all elements within a domain, establishing strong semantic constraints crucial for formal verification and ontology design. Disjunctive property allows a condition to be satisfied by at least one element among many, supporting flexible reasoning and efficient query processing in knowledge representation systems. Balancing these properties optimizes semantic precision and computational tractability in automated reasoning and data integration tasks.
Conclusion: Choosing the Right Property for Your Analysis
Selecting between the Universal property and Disjunctive property depends on the scope and specificity of the analysis. Universal properties apply broadly across all elements, ensuring comprehensive insight, whereas Disjunctive properties target specific, mutually exclusive conditions for more precise differentiation. For holistic data interpretation, Universal properties are ideal, while Disjunctive properties suit focused, conditional assessments in semantic and logical frameworks.
Universal property Infographic
 libterm.com
libterm.com