A definite description uniquely identifies a specific entity within a given context, such as "the tallest building in the city." It plays a crucial role in semantics by enabling precise reference and eliminating ambiguity in communication. Explore the article to understand how definite descriptions function in language and logic.
Table of Comparison
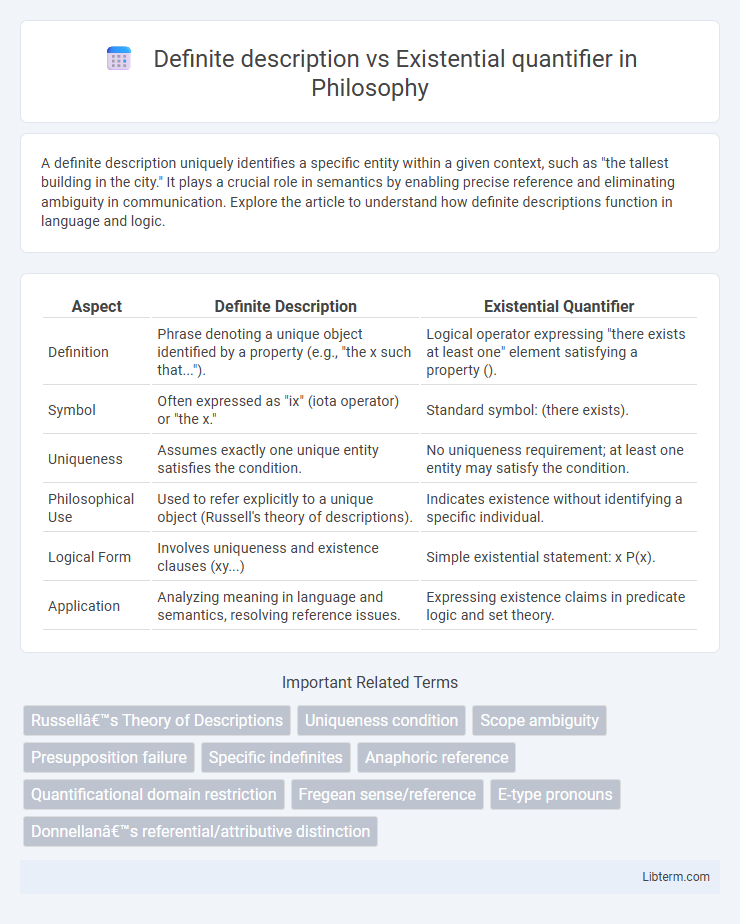
| Aspect | Definite Description | Existential Quantifier |
|---|---|---|
| Definition | Phrase denoting a unique object identified by a property (e.g., "the x such that..."). | Logical operator expressing "there exists at least one" element satisfying a property (). |
| Symbol | Often expressed as "ix" (iota operator) or "the x." | Standard symbol: (there exists). |
| Uniqueness | Assumes exactly one unique entity satisfies the condition. | No uniqueness requirement; at least one entity may satisfy the condition. |
| Philosophical Use | Used to refer explicitly to a unique object (Russell's theory of descriptions). | Indicates existence without identifying a specific individual. |
| Logical Form | Involves uniqueness and existence clauses (xy...) | Simple existential statement: x P(x). |
| Application | Analyzing meaning in language and semantics, resolving reference issues. | Expressing existence claims in predicate logic and set theory. |
Introduction to Definite Descriptions
Definite descriptions specify a unique entity within a given context, often expressed using the phrase "the" followed by a noun, such as "the president." Existential quantifiers denote the existence of at least one entity satisfying a property, symbolized as x, meaning "there exists an x." Understanding definite descriptions involves analyzing their role in identifying singular objects distinct from the broader existential claims made by quantifiers.
Understanding the Existential Quantifier
The existential quantifier () in logic asserts the existence of at least one element in a domain that satisfies a given property, contrasting with definite descriptions which specify a unique entity. Understanding the existential quantifier involves recognizing its role in expressing "there exists" statements, foundational for formulating propositions in predicate logic. Mastery of existential quantification enhances the ability to handle proofs, model theories, and reason about sets and their members effectively.
Historical Background and Key Philosophers
The concepts of definite description and existential quantifier originated from formal logic and philosophy of language, with Bertrand Russell's 1905 theory of definite descriptions providing a systematic analysis of phrases like "the current king of France," contrasting with the existential quantifier's role in predicate logic symbolizing "there exists" () to express existence claims. Key philosophers such as Gottlob Frege influenced early logical formalism and semantic frameworks, while Rudolf Carnap and Alfred Tarski contributed to the development of quantification theory and semantic interpretation. This foundational work shaped modern analytic philosophy, formal semantics, and mathematical logic by clarifying the distinctions between reference, existence, and uniqueness in language.
Syntax and Semantics of Definite Descriptions
Definite descriptions have a syntactic structure typically represented as "the F," where F is a predicate indicating uniqueness, while existential quantifiers use expressions like "there exists an x such that F(x)" to assert existence without uniqueness. Semantically, definite descriptions presuppose the existence and uniqueness of an entity satisfying the predicate, handled via Russellian analysis or alternative frameworks like the E-type theory. The distinction lies in the definite description's requirement that exactly one entity fulfills the description, contrasting with the existential quantifier's weaker claim of at least one entity's existence.
Formalizing the Existential Quantifier
The existential quantifier () in formal logic asserts the existence of at least one element in a domain that satisfies a given predicate, enabling precise statements about existence without identifying specific elements. Definite descriptions, often formalized using the iota operator (i), specify a unique element meeting certain criteria, distinguishing them from existential quantifiers that do not guarantee uniqueness. Formalizing the existential quantifier involves translating natural language existence claims into expressions such as x P(x), which is fundamental in predicate logic for proving the presence of elements with desired properties.
Comparative Analysis: Definite Description vs Existential Quantifier
Definite descriptions specify a unique entity that satisfies a given property, formalized as "the x such that P(x)," while existential quantifiers assert the existence of at least one entity meeting the condition P(x), expressed as "there exists an x such that P(x)." Definite descriptions imply uniqueness and singular reference, enabling precise identification within a domain, whereas existential quantifiers allow for multiple or unspecified instances without guaranteeing singularity. The semantic distinction impacts logical interpretations and linguistic applications, with definite descriptions crucial for definite noun phrases and existential quantifiers underpinning existence claims in predicate logic.
Logical Role in Quantification Theory
Definite descriptions uniquely specify an entity within a domain, enabling precise reference in logical formulas, while existential quantifiers express the existence of at least one entity satisfying a property without uniqueness. In quantification theory, definite descriptions serve to isolate a singular individual, supporting statements that imply uniqueness and existence simultaneously, whereas existential quantifiers validate assertions about non-empty sets. The logical role of definite descriptions often involves transforming natural language phrases into formal expressions that capture both existence and uniqueness, contrasting with the broader scope of existential quantifiers that lack specificity about uniqueness.
Common Misconceptions and Clarifications
Definite descriptions, symbolized as ix, assert the existence of a unique entity satisfying a property, unlike existential quantifiers (x) which only claim at least one such entity exists. A common misconception is treating definite descriptions as simple existential statements, ignoring uniqueness and leading to ambiguity in logical analysis. Clarifying this distinction ensures precise formalization in semantics, where definite descriptions require both existence and uniqueness conditions, while existential quantifiers only require existence.
Applications in Linguistics and Logic
Definite descriptions, such as "the king of France," refer to a unique entity assumed to exist, playing a crucial role in semantics for specifying particular objects in linguistic analysis. Existential quantifiers express the existence of at least one entity satisfying a given property, fundamental in predicate logic for formulating statements about groups or objects without specifying uniqueness. In linguistics, definite descriptions help model specificity and presupposition in discourse, while existential quantifiers underpin the interpretation of indefinite noun phrases and scope relations in logical syntax and semantics.
Conclusion and Future Directions
Definite descriptions uniquely identify entities within a domain, enabling precise reference in logical and linguistic frameworks, whereas existential quantifiers assert the existence of at least one entity satisfying a given property without specifying uniqueness. Future research aims to refine the integration of definite descriptions with existential quantifiers in formal semantics to enhance natural language understanding systems and improve automated reasoning in knowledge representation. Advances in computational linguistics and formal logic are expected to develop hybrid models that leverage the strengths of both concepts for more robust semantic interpretation.
Definite description Infographic
 libterm.com
libterm.com