Absolute values represent the magnitude of a number without considering its sign, crucial in fields like mathematics and engineering for measuring distance or magnitude effectively. Understanding how absolute values function can simplify solving equations and analyzing real-world problems involving measurement. Dive into the rest of the article to enhance your grasp of absolute values and their practical applications.
Table of Comparison
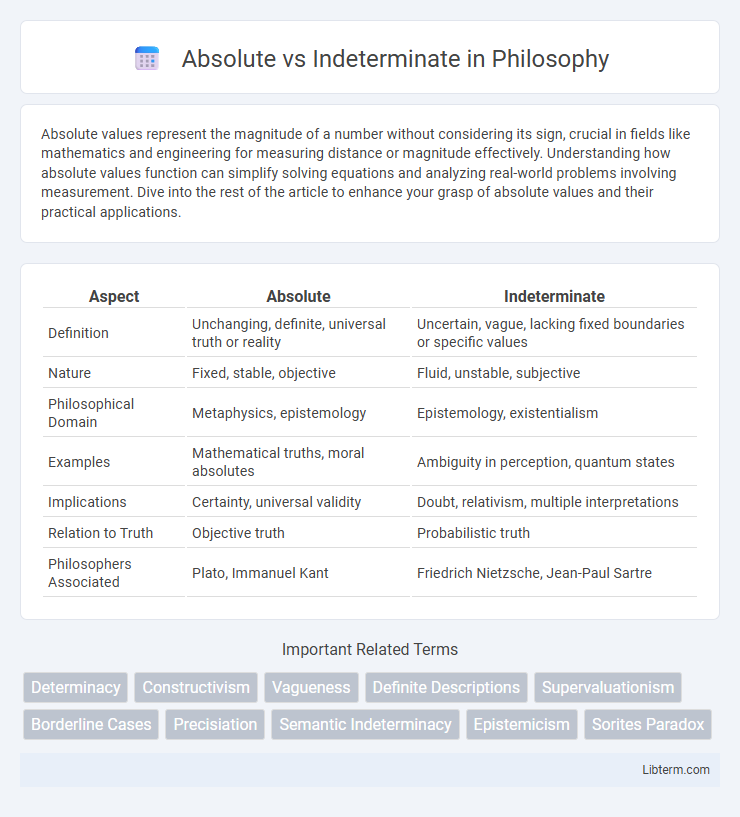
| Aspect | Absolute | Indeterminate |
|---|---|---|
| Definition | Unchanging, definite, universal truth or reality | Uncertain, vague, lacking fixed boundaries or specific values |
| Nature | Fixed, stable, objective | Fluid, unstable, subjective |
| Philosophical Domain | Metaphysics, epistemology | Epistemology, existentialism |
| Examples | Mathematical truths, moral absolutes | Ambiguity in perception, quantum states |
| Implications | Certainty, universal validity | Doubt, relativism, multiple interpretations |
| Relation to Truth | Objective truth | Probabilistic truth |
| Philosophers Associated | Plato, Immanuel Kant | Friedrich Nietzsche, Jean-Paul Sartre |
Introduction to Absolute and Indeterminate Concepts
Absolute concepts refer to definitive, unchanging values or states that are universally accepted and verifiable, such as mathematical constants like pi or physical laws like gravity. Indeterminate concepts embody uncertainty or variability, lacking precise boundaries or outcomes, often seen in quantum mechanics or probabilistic events. Understanding the distinction is crucial in fields like philosophy, science, and law, where clarity between fixed truths and variable interpretations shapes analysis and decision-making.
Defining Absolute: Meaning and Applications
Absolute refers to a state or condition that is complete, unconditional, and independent of any external factors or limitations. In various fields such as mathematics, philosophy, and law, absolute indicates something that is universally valid, definite, and not subject to change or interpretation. Applications of absolute concepts include absolute truth in philosophy, absolute zero in physics, and absolute liability in legal contexts, emphasizing their foundational and non-relative nature.
Understanding Indeterminate: Definition and Contexts
Indeterminate refers to situations or values that lack a fixed, well-defined quantity or outcome, often arising in mathematics, biology, and legal contexts. In calculus, indeterminate forms like 0/0 occur during limits, requiring specialized methods such as L'Hopital's Rule to resolve. In legal terms, indeterminate sentences lack a set duration, emphasizing rehabilitation over punishment, highlighting the variable nature of the concept across disciplines.
Historical Perspectives on Absolute and Indeterminate
Historical perspectives on the concepts of Absolute and Indeterminate trace back to ancient philosophy, where Absolute often represented unchanging, universal truths, while Indeterminate signified the unknown or variable elements of reality. Greek philosophers such as Plato emphasized the Absolute through ideal forms, contrasting with Heraclitus's focus on flux and change, which aligns more with Indeterminate. The evolution of these ideas continued through medieval scholasticism and Enlightenment thought, shaping debates on certainty, existence, and the nature of knowledge.
Key Differences Between Absolute and Indeterminate
Absolute concepts refer to fixed, clearly defined states that do not allow for variation or ambiguity, whereas indeterminate concepts are characterized by uncertainty, variability, or lack of precise limits. Absolute measurements or truths are definitive and unchanging, while indeterminate cases often require interpretation and allow for multiple possible outcomes. The key difference lies in absolutes providing exactness and certainty, while indeterminates embody flexibility and uncertainty within defined boundaries.
Philosophical Implications of Absolutism and Indeterminacy
Absolutism in philosophy asserts that certain truths or moral principles are universally valid, grounded in objective reality regardless of context or perception. Indeterminacy challenges this notion by emphasizing ambiguity, context-dependent meanings, and the limits of definitive knowledge, often linked to linguistic and metaphysical uncertainty. The tension between absolutism and indeterminacy raises critical questions about the nature of truth, knowledge, and ethical objectivity, influencing debates in epistemology, ethics, and metaphysics.
Absolute vs Indeterminate in Mathematics and Science
In Mathematics and Science, absolute values represent precise, fixed quantities such as the absolute value of a number indicating its distance from zero on the number line, regardless of direction. Indeterminate forms, common in limits and calculus, occur when expressions like 0/0 or / do not have a clearly defined value and require further analysis through methods like L'Hopital's rule. Understanding the distinction is crucial for solving equations, evaluating limits, and interpreting measurement data where exactness versus ambiguity significantly impacts results.
Examples of Absolute and Indeterminate in Real Life
Absolute examples in real life include laws like gravity, where objects consistently fall toward the Earth, and mathematical truths such as 2+2=4, which hold universally without exception. Indeterminate situations appear in weather forecasts predicting rain with a probability of 60%, or in legal cases where evidence is inconclusive, leaving verdicts uncertain. These contrasts illustrate how absolute concepts are fixed and predictable, whereas indeterminate ones depend on varying conditions and probabilities.
Impacts of Absolute and Indeterminate Thinking
Absolute thinking rigidly categorizes experiences into black-and-white terms, often leading to increased stress, anxiety, and impaired decision-making due to its inflexibility. Indeterminate thinking, characterized by openness to ambiguity and uncertainty, fosters adaptability, creative problem-solving, and emotional resilience. Understanding the psychological impacts of these cognitive styles is crucial for mental health interventions and improving cognitive flexibility in diverse contexts.
Conclusion: Navigating Between the Absolute and the Indeterminate
Navigating between the absolute and the indeterminate involves recognizing the value of certainty while embracing flexibility in complex situations. Absolute positions offer clarity and definitive answers, essential for firm decision-making and foundational principles. Indeterminate perspectives allow adaptation and openness, which are crucial in dynamic environments where ambiguity fosters innovation and growth.
Absolute Infographic
 libterm.com
libterm.com