Understanding the various types of property, including real estate, personal property, and intellectual property, is essential for making informed decisions about ownership and investment. Knowing your rights and responsibilities can help protect your assets and maximize their value. Explore the rest of the article to learn how to manage and leverage your property effectively.
Table of Comparison
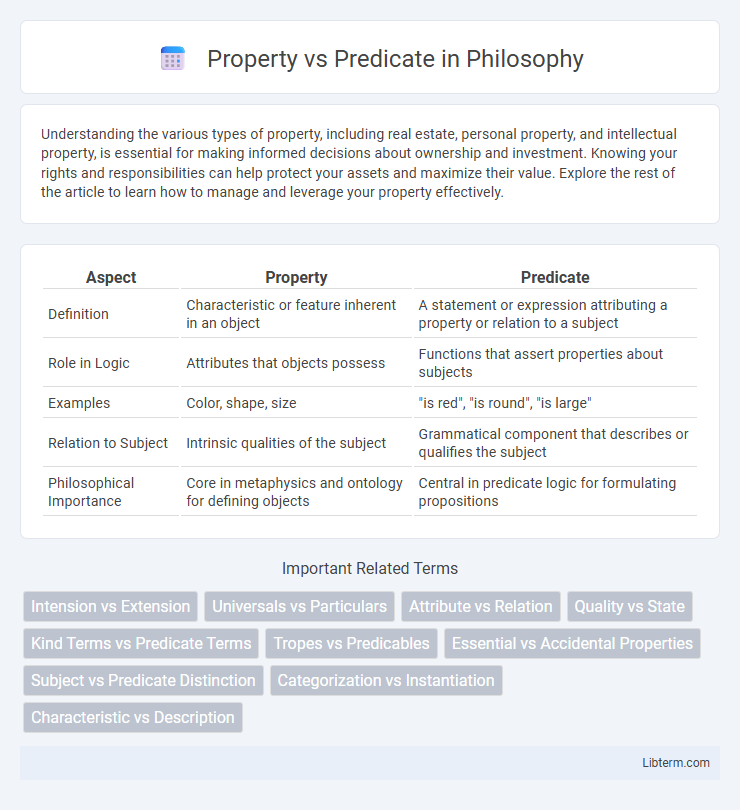
| Aspect | Property | Predicate |
|---|---|---|
| Definition | Characteristic or feature inherent in an object | A statement or expression attributing a property or relation to a subject |
| Role in Logic | Attributes that objects possess | Functions that assert properties about subjects |
| Examples | Color, shape, size | "is red", "is round", "is large" |
| Relation to Subject | Intrinsic qualities of the subject | Grammatical component that describes or qualifies the subject |
| Philosophical Importance | Core in metaphysics and ontology for defining objects | Central in predicate logic for formulating propositions |
Introduction to Property and Predicate
A property in programming and logic refers to an attribute or characteristic that an object or entity possesses, such as color, size, or age. A predicate, on the other hand, is a function or expression that evaluates to true or false based on the properties of an object or the relationships among objects. Understanding the distinction between property as a descriptive feature and predicate as a test or condition is essential in fields like predicate logic, object-oriented programming, and database querying.
Defining Properties in Logic
Defining properties in logic involves assigning specific attributes or qualities to objects within a domain, often expressed as predicates that map objects to truth values. A property represents a unary predicate indicating whether an object possesses a certain characteristic, enabling formal reasoning about object attributes. This distinction between properties and predicates is crucial for constructing precise logical statements and semantic interpretations.
Understanding Predicates in Semantics
Predicates in semantics represent the actions, states, or relations attributed to a subject, distinguishing them from properties, which denote inherent qualities or characteristics. Understanding predicates involves analyzing their role in structuring meaning within sentences, often encapsulated by verbs and verb phrases that express what the subject does or experiences. This distinction is crucial for semantic parsing and natural language processing, as predicates define the dynamic aspects of propositions and their truth conditions.
Key Differences: Property vs Predicate
Properties describe attributes or qualities of an entity, such as color, size, or shape, defining characteristics that can be measured or observed. Predicates function as statements or expressions in logic and linguistics, asserting relationships, actions, or states involving one or more entities, typically forming the main part of a sentence or proposition. The key difference lies in properties representing static traits, while predicates indicate dynamic relations or conditions applied to entities.
Role of Properties in Formal Languages
In formal languages, properties serve as fundamental predicates that define essential characteristics or attributes of objects within a domain. They enable precise specification of conditions and constraints, facilitating rigorous reasoning and verification processes. By representing properties as predicates, formal languages support unambiguous interpretation and manipulation of data structures, contributing to sound logical frameworks and automated theorem proving.
Predicates in Predicate Logic
Predicates in predicate logic represent properties or relations applied to one or more subjects, serving as functions that return truth values depending on the arguments provided. Unlike simple properties that denote characteristics of objects, predicates express more complex statements involving variables and quantifiers, enabling formal reasoning about object relationships and attributes. They are fundamental in constructing logical formulas that capture detailed conditions and allow inference mechanisms within mathematical logic and computer science.
Examples Illustrating Properties and Predicates
A property in logic refers to a characteristic or attribute that an object can have, such as "red" or "tall," while a predicate expresses a statement or relation involving one or more subjects, for example, "is red" or "is taller than." For instance, in the sentence "The apple is red," "red" is a property attributed to the apple, whereas in "John is taller than Mary," the predicate "is taller than" relates two subjects, John and Mary. Analyzing these examples clarifies that properties are qualities owned by objects, whereas predicates function as expressions that can assign properties or define relationships among entities.
Applications in Mathematics and Computer Science
Properties serve as attributes that characterize elements within a set, while predicates are functions that return truth values based on those attributes. In mathematics, predicates are essential for defining subsets and formulating logical statements, such as in predicate logic and set theory. Computer science leverages predicates in algorithms, database querying, and program verification to evaluate conditions and enforce constraints efficiently.
Common Misconceptions and Clarifications
A common misconception confuses properties with predicates, assuming they are interchangeable in logic and computer science. A property represents an attribute or characteristic inherent to an entity, such as "red" or "tall," while a predicate is a function or relation that evaluates to true or false based on the entity's properties, like "is red" or "is taller than." Clarifying this distinction is essential for accurate semantic modeling, ontology design, and formal logic applications.
Conclusion: Significance in Semantics and Logic
The distinction between property and predicate is fundamental in semantics and logic, as properties represent inherent characteristics or attributes of entities, while predicates function as linguistic tools to express these properties within propositions. Understanding this difference enhances clarity in formal reasoning, allowing precise interpretation and manipulation of statements in logical systems. The significance lies in enabling more accurate modeling of meaning and facilitating robust semantic analysis across computational linguistics and philosophical logic.
Property Infographic
 libterm.com
libterm.com