Modal logic explores concepts of necessity and possibility through formal systems that extend classical logic with modal operators. It has applications in philosophy, computer science, linguistics, and artificial intelligence, helping to model knowledge, belief, time, and obligation. Discover how modal logic can enhance your understanding of reasoning and unlock new perspectives by reading the rest of the article.
Table of Comparison
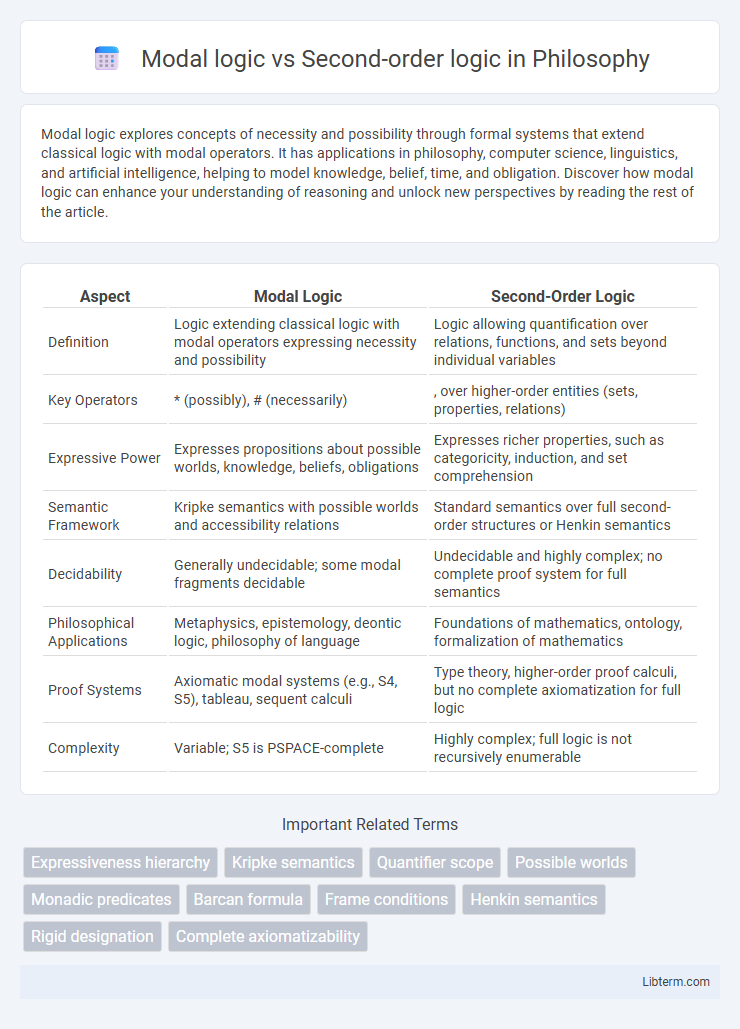
| Aspect | Modal Logic | Second-Order Logic |
|---|---|---|
| Definition | Logic extending classical logic with modal operators expressing necessity and possibility | Logic allowing quantification over relations, functions, and sets beyond individual variables |
| Key Operators | * (possibly), # (necessarily) | , over higher-order entities (sets, properties, relations) |
| Expressive Power | Expresses propositions about possible worlds, knowledge, beliefs, obligations | Expresses richer properties, such as categoricity, induction, and set comprehension |
| Semantic Framework | Kripke semantics with possible worlds and accessibility relations | Standard semantics over full second-order structures or Henkin semantics |
| Decidability | Generally undecidable; some modal fragments decidable | Undecidable and highly complex; no complete proof system for full semantics |
| Philosophical Applications | Metaphysics, epistemology, deontic logic, philosophy of language | Foundations of mathematics, ontology, formalization of mathematics |
| Proof Systems | Axiomatic modal systems (e.g., S4, S5), tableau, sequent calculi | Type theory, higher-order proof calculi, but no complete axiomatization for full logic |
| Complexity | Variable; S5 is PSPACE-complete | Highly complex; full logic is not recursively enumerable |
Introduction to Modal Logic and Second-order Logic
Modal logic extends classical propositional and predicate logic by introducing modalities such as necessity and possibility, represented through operators like (necessarily) and * (possibly). Second-order logic expands first-order logic by quantifying not only over individual variables but also over predicates, functions, and sets, allowing for a richer expressive power to capture properties and relations about properties themselves. While modal logic emphasizes the semantics of modality and possible worlds, second-order logic provides a framework to express statements about collections and higher-level abstractions beyond the capabilities of first-order logic.
Fundamental Concepts in Modal Logic
Modal logic centers on the concepts of necessity and possibility, employing modal operators such as * (possibly) and # (necessarily) to express statements beyond classical truth values. It introduces possible world semantics, where the truth of propositions depends on their validity across various accessible worlds, distinguishing it from second-order logic's broader quantification over sets or relations. Fundamental concepts include accessibility relations, Kripke frames, and the distinction between modal axioms, which systematically characterize different modal systems based on constraints on these frames.
Essential Features of Second-order Logic
Second-order logic extends first-order logic by quantifying not only over individual variables but also over relations, functions, and sets, enabling more expressive power in formal systems compared to modal logic. Unlike modal logic, which introduces possible worlds semantics to handle necessity and possibility, second-order logic's essential feature is its capacity to capture properties and concepts that first-order logic cannot, such as categoricity of number theory and real analysis axioms. This characteristic allows second-order logic to express higher-level abstractions and mathematical truths with greater precision and completeness.
Syntax Comparison: Modal vs Second-order Logic
Modal logic employs a syntax centered on modal operators such as * (diamond) and # (box) to express necessity and possibility, extending propositional logic with these unary operators. Second-order logic syntax includes quantifiers over not only individual variables but also predicates and functions, allowing for quantification over sets and relations. Unlike modal logic's use of modal operators to navigate possible worlds semantics, second-order logic's syntax directly captures higher-order properties through its enriched quantificational structure.
Semantic Differences: Modality and Quantification
Modal logic emphasizes the semantics of necessity and possibility through possible world frameworks, interpreting modal operators like * (possibly) and # (necessarily) across varying accessible worlds. Second-order logic extends first-order logic by quantifying over sets, relations, or functions, allowing variables to represent not only elements but also subsets of the domain, enabling richer expressive power. The key semantic difference lies in modal logic's focus on varying truth values across possible worlds, whereas second-order logic expands expressiveness by quantifying over higher-order entities within a single fixed domain.
Expressive Power: Limits and Capabilities
Modal logic offers a specialized expressive framework for reasoning about necessity and possibility, effectively capturing concepts like temporal, epistemic, and deontic modalities. Second-order logic significantly extends expressive power beyond first-order or modal logics by allowing quantification over predicates and sets, enabling the characterization of properties and structures that modal logic cannot express. While modal logic is decidable and computationally simpler, second-order logic's expressive capabilities are richer but generally undecidable, marking a fundamental trade-off between expressive power and computational tractability.
Applications in Mathematics and Philosophy
Modal logic provides powerful tools for reasoning about necessity and possibility, widely applied in metaphysics and epistemology to analyze statements about knowledge, belief, and time. Second-order logic extends first-order logic by quantifying over relations and properties, enabling a more expressive framework crucial for formalizing mathematics, including categoricity results and foundational theories. In mathematics, second-order logic captures structures such as arithmetic and real analysis more completely, while in philosophy, modal logic addresses modal metaphysics and counterfactual reasoning, making both systems indispensable for their respective domains.
Model Theory Perspectives
Modal logic emphasizes possible worlds semantics, using accessibility relations to interpret necessity and possibility, which allows for elegant model-theoretic analysis of modal operators. Second-order logic extends classical first-order logic by quantifying over relations and sets, increasing expressiveness but sacrificing some desirable model-theoretic properties such as compactness and completeness. From a model theory perspective, modal logic offers tractable frames and robust completeness theorems, whereas second-order logic's expressive power leads to more complex, often non-recursive model classes, complicating its semantic analysis.
Computational Complexity and Decidability
Modal logic typically exhibits lower computational complexity and greater decidability compared to second-order logic, as modal formulas can often be decided within PSPACE or EXPTIME, depending on the system. In contrast, second-order logic is highly expressive with undecidable validity problems, leading to non-recursive enumerability and generally higher complexity classes beyond the arithmetical hierarchy. The decidability and complexity gap reflects the trade-off between expressiveness and algorithmic tractability inherent in these logics.
Conclusion: Choosing the Right Logic Framework
Choosing between modal logic and second-order logic depends on the specific application requirements; modal logic excels in expressing necessity, possibility, and temporal reasoning with computational efficiency, while second-order logic offers greater expressive power to quantify over sets and relations but at the cost of undecidability and higher complexity. Modal logic frameworks are well-suited for systems modeling, knowledge representation, and verification tasks where tractability is crucial. In contrast, second-order logic is preferable for theoretical foundations, formal semantics, and contexts demanding rich expressiveness despite computational limitations.
Modal logic Infographic
 libterm.com
libterm.com