Logical consequence defines the relationship between statements where one assertion necessarily follows from others based on formal logic rules. This concept is fundamental in reasoning, mathematics, and computer science to ensure valid argument structures and sound conclusions. Explore the rest of the article to deepen your understanding of logical consequence and its applications.
Table of Comparison
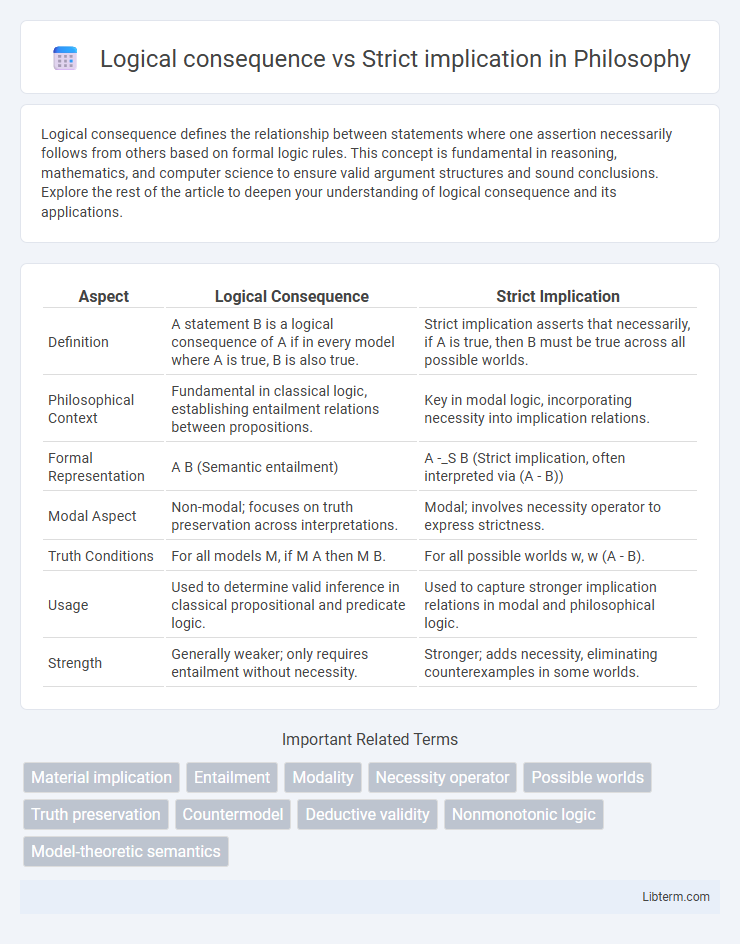
| Aspect | Logical Consequence | Strict Implication |
|---|---|---|
| Definition | A statement B is a logical consequence of A if in every model where A is true, B is also true. | Strict implication asserts that necessarily, if A is true, then B must be true across all possible worlds. |
| Philosophical Context | Fundamental in classical logic, establishing entailment relations between propositions. | Key in modal logic, incorporating necessity into implication relations. |
| Formal Representation | A B (Semantic entailment) | A -_S B (Strict implication, often interpreted via (A - B)) |
| Modal Aspect | Non-modal; focuses on truth preservation across interpretations. | Modal; involves necessity operator to express strictness. |
| Truth Conditions | For all models M, if M A then M B. | For all possible worlds w, w (A - B). |
| Usage | Used to determine valid inference in classical propositional and predicate logic. | Used to capture stronger implication relations in modal and philosophical logic. |
| Strength | Generally weaker; only requires entailment without necessity. | Stronger; adds necessity, eliminating counterexamples in some worlds. |
Understanding Logical Consequence
Logical consequence refers to a relationship between premises and conclusion where the conclusion must be true if the premises are true, emphasizing truth preservation in formal logic systems. It is a fundamental concept in model theory and proof theory, ensuring valid inference across all interpretations. Strict implication, by contrast, involves a stronger modal operator indicating necessity, but understanding logical consequence is crucial for grasping how validity and inferential soundness are established in logical frameworks.
Defining Strict Implication
Strict implication is a modal logical relation asserting that if the antecedent is true, the consequent must necessarily be true in all possible worlds, reflecting a stronger connection than logical consequence. Unlike logical consequence, which is a meta-logical notion about truth preservation across interpretations, strict implication operates within the formal system using modal operators to express necessity. This distinction emphasizes strict implication's role in capturing necessary entailment rather than mere truth preservation.
Historical Development of Logical Implication
The historical development of logical implication reveals a distinction between logical consequence and strict implication rooted in the works of Frege, Russell, and later modal logicians. Logical consequence, formalized in proof theory, captures the semantic entailment where the truth of premises guarantees the truth of conclusions, while strict implication introduced by C.I. Lewis incorporates necessity, emphasizing modal logic frameworks. This evolution reflects the shift from purely truth-functional interpretations to incorporating necessity and modality in understanding logical implication.
Syntax and Semantics: Key Differences
Logical consequence pertains to the semantic relationship where a conclusion necessarily follows from premises based on truth preservation in all models, whereas strict implication is a syntactic construct expressing necessity within modal logic. Logical consequence is defined by entailment in model theory, emphasizing truth across all interpretations, while strict implication relies on modal operators within formal proofs to establish necessity. The key difference lies in logical consequence operating at the level of semantic entailment, contrasting with strict implication's role as a formal syntactic operator embedded in modal logic systems.
Formal Systems: Proof Theory vs Model Theory
Logical consequence in Formal Systems refers to the relationship where a statement necessarily follows from a set of premises within a deductive framework, primarily studied in Proof Theory through syntactic derivations and proof procedures. Strict implication, on the other hand, is a modal concept often analyzed within Model Theory, capturing necessity across possible worlds and emphasizing semantic entailment rather than mechanical proof. Proof Theory focuses on the construction of proofs as sequences of inference steps, while Model Theory examines the truth of statements across interpretations, highlighting the distinction between syntactic derivability and semantic validity.
Examples Illustrating Logical Consequence
Logical consequence occurs when a conclusion necessarily follows from premises, such as if "All humans are mortal" and "Socrates is a human," then "Socrates is mortal" is logically entailed. In contrast, strict implication involves modal necessity, meaning a statement A strictly implies B if in every possible world where A is true, B is true as well. For example, the logical consequence "If it is raining, then the ground is wet" holds in actual world reasoning, while strict implication requires this to be true in all conceivable scenarios.
Examples Illustrating Strict Implication
Strict implication, symbolized as #(P - Q), means that in all possible worlds where P is true, Q must also be true, illustrating a necessity beyond mere truth preservation. For example, "If 2 is even (P), then 4 is even (Q)" is strictly implied since in every conceivable scenario where 2 is even, 4 is inevitably even. This contrasts with logical consequence, which only requires that Q be true whenever P is true in the actual world or a given model, not universally across all possible worlds.
Philosophical Implications of Each Concept
Logical consequence centers on the relationship between premises and conclusions, highlighting truth preservation across all interpretations, which underpins foundational debates in epistemology and logic. Strict implication, defined within modal logic, emphasizes necessity and possibility, raising questions about the nature of implication beyond mere truth-functionality, thus impacting theories of meaning and inference. Each concept informs philosophical discussions on how truth conditions relate to reasoning validity and the interpretation of communicative intention.
Challenges in Distinguishing Logical Consequence and Strict Implication
Distinguishing logical consequence from strict implication presents challenges due to their nuanced semantic differences and overlapping formal structures. Logical consequence emphasizes truth preservation under all interpretations in a model-theoretic framework, while strict implication focuses on necessity within modal logic, complicating their conceptual separation. Misinterpretations often arise from conflating syntactic derivations with semantic necessity, hindering clarity in formal proofs and philosophical analysis.
Practical Applications in Logic and Computer Science
Logical consequence underpins automated theorem proving and formal verification by ensuring that derived conclusions are semantically entailed by premises, making it essential in program correctness analysis and model checking. Strict implication, reflecting necessity modalities, informs the design of modal logics and type systems in programming languages, supporting reasoning about system behaviors over time and under varying conditions. Both concepts strengthen logic-based tools in artificial intelligence, enabling sophisticated inference mechanisms and knowledge representation frameworks for decision-making and problem-solving.
Logical consequence Infographic
 libterm.com
libterm.com